9  Pronóstico de decesos diarios

De manera similar a la evaluación llevada a cabo en la base de datos de los casos confirmados de COVID-19 en Irán, se ejecutó un análisis para los datos de muertes por COVID-19 en Irán, abarcando el mismo período temporal, desde el 20 de febrero hasta el 15 de agosto de 2020. El propósito fue determinar si, de forma análoga, la red neuronal MLP demuestra un mejor ajuste a los datos en comparación con la técnica de series temporales Holt-Winters, o si, en este caso particular, la técnica Holt-Winters ofrece una mayor precisión.

Es relevante señalar la presencia de datos faltantes para las fechas 21 de febrero, 1 de marzo y 5 de mayo de 2020 en el conjunto de datos. Por consiguiente, al igual que en los casos confirmados, se procedió con una interpolación promedio para sustituir dichos datos faltantes. La Figura 9.1 exhibe la serie temporal resultante luego de estas correcciones.

Figura 9.1: Serie de tiempo de los casos de muerte por COVID-19 en Irán del 20-02-2020 al 15-08-2020.

9.1 Pronóstico, comparación y métricas de rendimiento

La evaluación del desempeño de los métodos se realiza a través de la separación del conjunto de datos en entrenamiento y prueba. El set inicial, compuesto por el \(70\%\) de los datos, se emplea para el entrenamiento de los modelos, mientras que el \(30\%\) restante se reservará para llevar a cabo las pruebas pertinentes.

Deaths_ts <- ts(Deaths_ts,frequency=1) 
tsize <- round(0.7 * nrow(Deaths_df)) 
train_deaths <- window(Deaths_ts,end=tsize) 
test_deaths <- window(Deaths_ts,start=tsize+1)

Con el propósito de llevar a cabo un análisis cuantitativo exhaustivo, se presenta a continuación una tabla comparativa de los resultados derivados de las dos técnicas implementadas (después de realizar el entrenamiento, modelado y pronóstico), y la base de datos de prueba. Posteriormente, se exhiben gráficas representativas de estos resultados. En la Figura 9.2 se muestra el pronóstico mediante Holt-Winters acompañado de su respectivo intervalo de confianza. En contraste, en la Figura 9.3, la gráfica punteada en color rojo representa el comportamiento real de los datos, mientras que en azul se representa el pronóstico obtenido a través de la red MLP.

Tabla 9.1: Comparación de Resultados entre las técnicas y los datos reales para evaluar precisión

Figura 9.2: Pronóstico obtenido mediante la técnica de Holt-Winters.

Figura 9.3: Pronóstico obtenido mediante la red neuronal MLP.

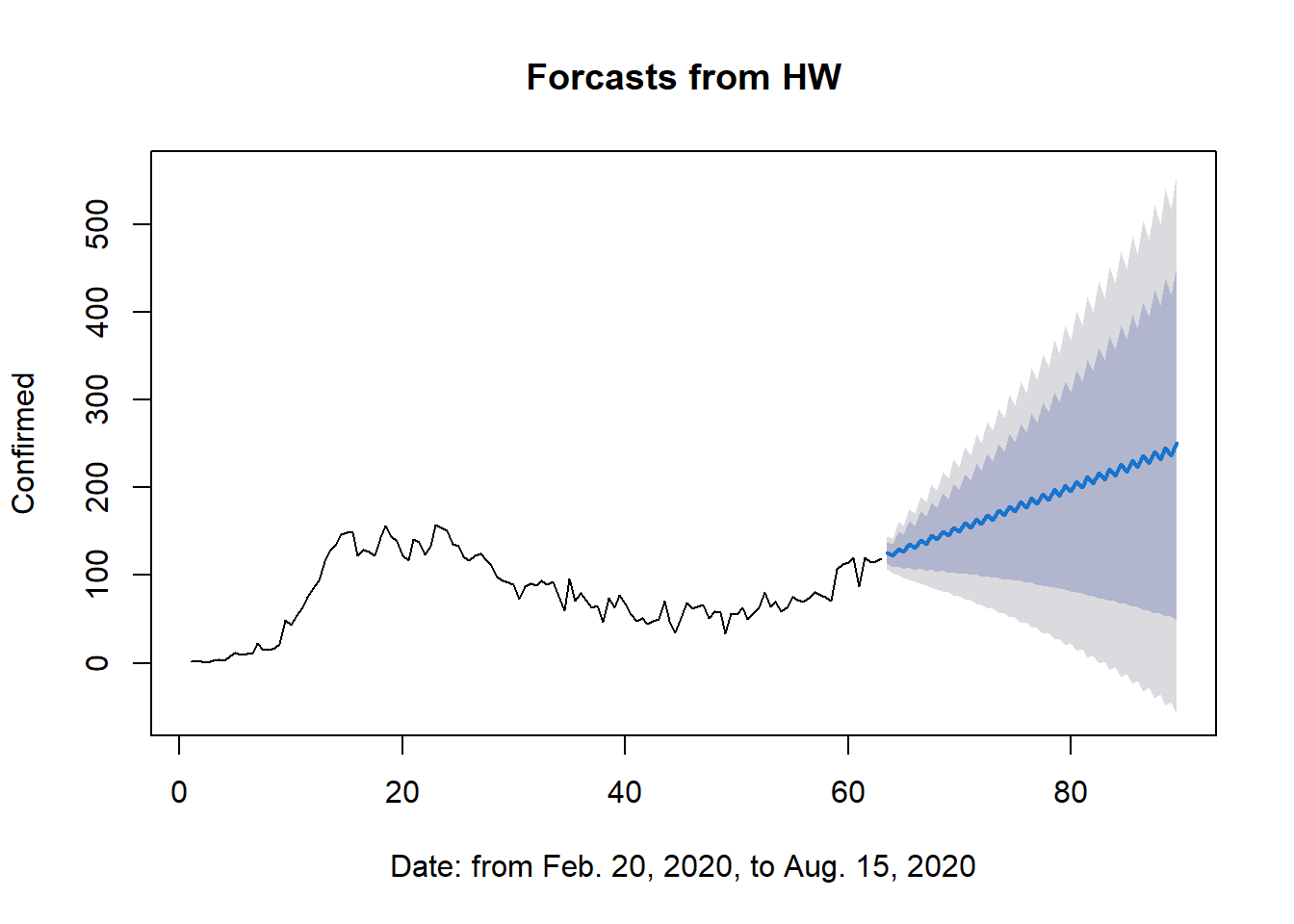
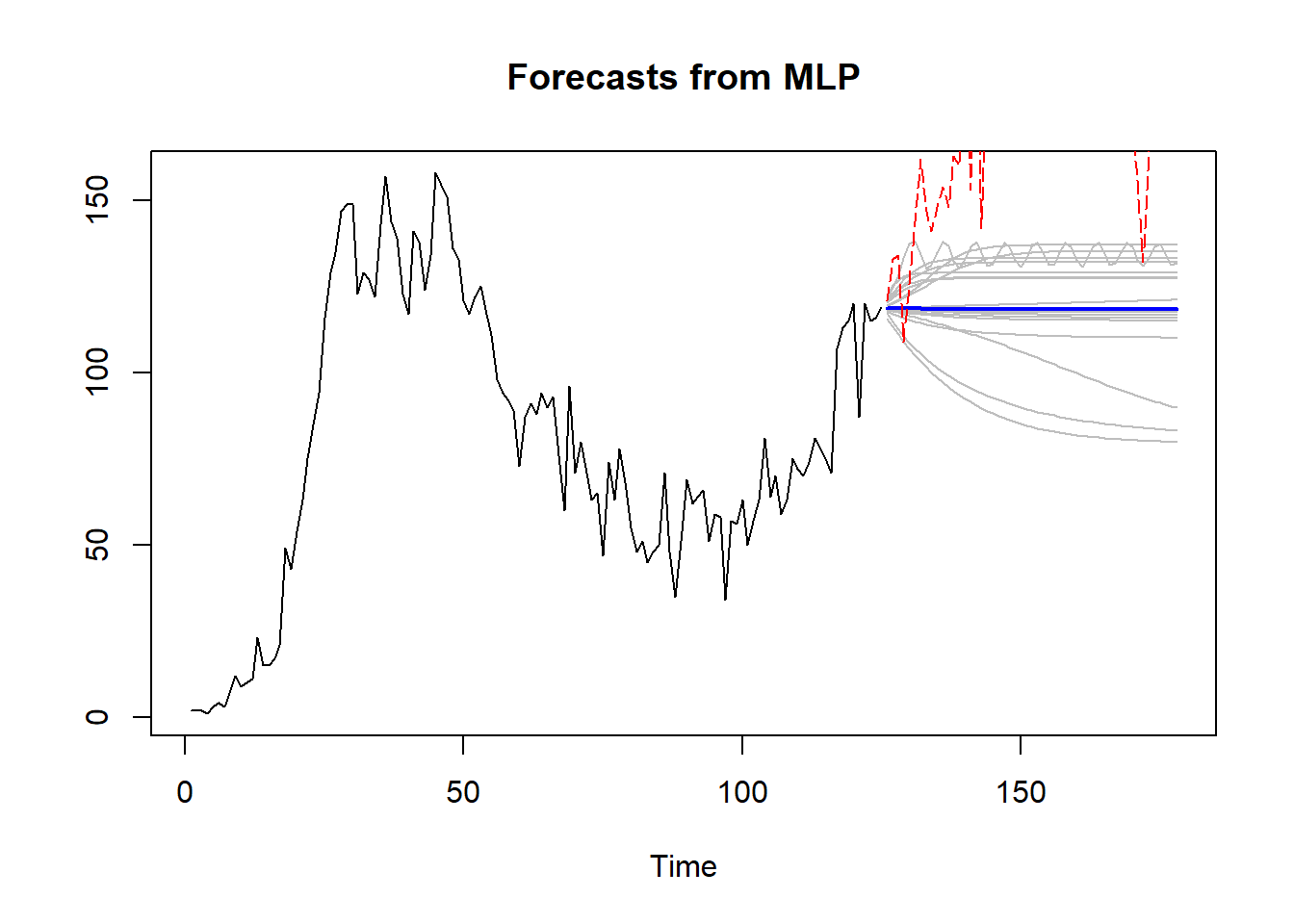
A través de las Figura 9.2 y Figura 9.3, se observa que el pronóstico derivado de la técnica Holt-Winters muestra una mayor proximidad al comportamiento de la gráfica real.

Utilizando las métricas RMSE, MAE y MAPE, se lleva a cabo la evaluación de la calidad o bondad de ajuste de los métodos empleados en este estudio con el fin de seleccionar el modelo más adecuado.

Tabla 9.2: Errores de los modelos para casos confirmados.

		Training			Testing
	RMSE	MAE	MAPE	RMSE	MAE	MAPE
Holt-Winters	12.6365	9.6103	19.4096	34.0665	25.5356	12.9770
MLP	11.7584	8.8446	15.6144	67.2031	59.7811	49.0686

Los resultados derivados de la tabla de errores (Tabla 9.2) llevan a la conclusión de que, en esta base de datos específica, a pesar de que la red MLP exhibe errores más reducidos durante la fase de entrenamiento, la técnica de Holt-Winters presenta un error considerablemente menor en la etapa de prueba en comparación con MLP. Esto evidencia su mayor eficacia en la predicción realizada. Por consiguiente, se recomienda el uso del método Holt-Winters para llevar a cabo el pronóstico de los próximos 30 días.

9.2 Pronóstico de los próximos 30 días

Tras la identificación del modelo óptimo, se procedió a prever el comportamiento futuro de la serie temporal de casos de muerte para los próximos 30 días utilizando dicho modelo. Se elaboraron representaciones gráficas de la predicción de estos casos, realizando una comparación de la efectividad entre las implementaciones de redes neuronales en la paquetería de R y la paquetería nativa de Python, las cuales se encuentran en las figuras Figura 9.4 y Figura 9.5, respectivamente.

9.2.1 Implementación en R

HW_deaths <- HoltWinters(ts(Deaths_df$Deaths,frequency = 2)) 
HW_for_d <- forecast(HW_deaths, h=30, level=c(80,95))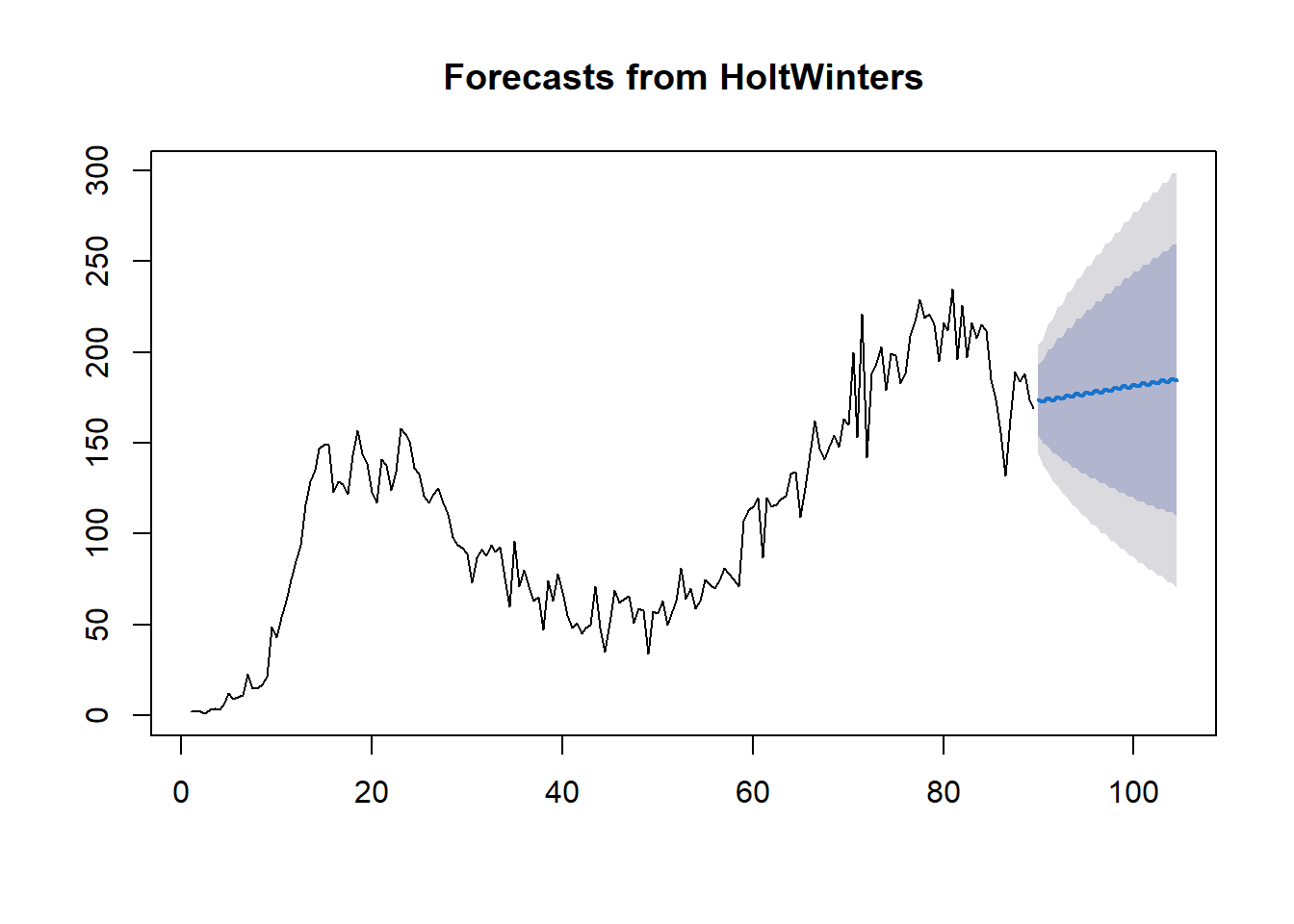 

Figura 9.4: Predicción futura de la serie tiempo para decesos diarios mediante el modelo Holt-Winters.

Los resultados del pronóstico indican que, el 14 de septiembre de 2020, se proyectan 184 nuevos casos de muerte por COVID-19. Estos valores correspondientes al período de 30 días se detallan a continuación en la Tabla 9.3 .

Tabla 9.3: Pronóstico de decesos por COVID-19 en Irán en los próximos 30 días.

9.2.2 Implementación en Python

▸Código

import numpy as np 
import pandas as pd 
import plotly.express as px 
from statsmodels.tsa.holtwinters import ExponentialSmoothing

# Importación de los datos de CASOS DE MUERTE del 20-02 al 15-08-2020
data = pd.read_excel('muertes.xlsx')
df = pd.DataFrame(data)

# Configurar el modelo Holt-Winters
model = ExponentialSmoothing(df['Deaths'], trend='add', 
seasonal='add',seasonal_periods=14)
model_fit = model.fit(optimized=True)

# Generar predicciones
forecast_days = 30  # Número de días a predecir
forecast = model_fit.forecast(steps=forecast_days)

# Crear un DataFrame con las fechas de predicción
forecast_dates = pd.date_range(start=df['Date'].max() + 
pd.Timedelta(days=1), periods=forecast_days, freq='D')

# Agregar las fechas y valores predichos al DataFrame original
forecast_df = pd.DataFrame({'Date': forecast_dates, 
'Forecast': forecast})
df_t = pd.concat([df, forecast_df])

# Crear una gráfica interactiva con Plotly
fig = px.line(df, x='Date', y='Deaths',title='Holt-Winters Forecast', 
labels={'Deaths': 'Deaths'})
fig.add_scatter(x=forecast_dates, y=forecast, mode='lines', 
name='Forecast', line=dict(color='red'))
fig.show()

Figura 9.5: Pronóstico de casos de muerte por COVID-19 en Irán en los próximos 30 días (implementación en Python).

Los resultados del pronóstico en la Figura 9.5 indican que, el 14 de septiembre de 2020, se proyectan aproximadamente 132 nuevos casos de muerte por COVID-19.