1  Teoría de conjuntos

En esta sección, se abordan algunas de las ideas y conceptos elementales de la teoría de conjuntos que son necesarios para una introducción moderna a la teoría de la probabilidad.

Se considera una colección de objetos en la que cada uno se denomina punto o elemento. Se asume que esta colección es lo suficientemente amplia como para incluir todos los puntos considerados en una discusión específica. La totalidad de estos puntos se conoce como espacio, universo o conjunto universal.

Se llamará al espacio (anticipando que se convertirá en el espacio muestral cuando se hable de probabilidad) y se denotará por \(\Omega\). Sea \(\omega\) un elemento o punto en \(\Omega\). Aunque un conjunto puede definirse como cualquier colección de objetos, se asumirá, a menos que se indique lo contrario, que todos los conjuntos mencionados en una discusión dada consisten en puntos en el espacio \(\Omega\).

\(\Omega = \mathbb{R}^2\), donde \(\mathbb{R}^2\) es la colección de puntos \(\omega\) en el plano y \(\omega=(x,y)\) es cualquier par de números reales \(x\) e \(y\).

Por lo general, se utilizarán letras latinas mayúsculas al comienzo del alfabeto, con o sin subíndices, para denotar conjuntos. Si \(\omega\) es un punto o elemento que pertenece al conjunto \(A\), se escribirá \(\omega \in A\); si \(\omega\) no es un elemento de \(A\), se escribirá \(\omega \notin A\).

Definición 1.1 (Subconjunto) Si cada elemento de un conjunto \(A\) también es un elemento de un conjunto \(B\), entonces se define que \(A\) es un subconjunto de \(B\), y se escribirá \(A\subset B\) o \(B\supset A\); se lee como “\(A\) está contenido en \(B\)” o “\(B\) contiene a \(A\)”.

Definición 1.2 (Conjuntos equivalentes) Dos conjuntos \(A\) y \(B\) se definen como equivalentes, o iguales, si \(A\subset B\) y \(B\subset A\). Esto se indicará escribiendo \(A=B\).

Definición 1.3 (Conjunto vacío) Si un conjunto \(A\) no contiene puntos, se le llamará conjunto nulo o conjunto vacío, y se denotará por \(\emptyset\).

Definición 1.4 (Complemento) El complemento de un conjunto \(A\) con respecto al espacio \(\Omega\), denotado por \(\overline{A}\), \(A^c\) o \(\Omega-A\), es el conjunto de todos los puntos que están en \(\Omega\) pero no en \(A\).

Definición 1.5 (Unión) Sean \(A\) y \(B\) dos subconjuntos cualesquiera de \(\Omega\); entonces el conjunto que consiste en todos los puntos que están en \(A\), en \(B\) o en ambos se define como la unión de \(A\) y \(B\), y se escribe \(A \cup B\).

Definición 1.6 (Intersección) Sean \(A\) y \(B\) dos subconjuntos cualesquiera de \(\Omega\); entonces el conjunto formado por todos los puntos que están tanto en \(A\) como en \(B\) se define como la intersección de \(A\) y \(B\), y se escribe \(A \cap B\).

Definición 1.7 (Diferencia de conjuntos) Sean \(A\) y \(B\) dos subconjuntos cualesquiera de \(\Omega\). Se define la diferencia de \(A\) y \(B\), denotada por \(A-B\), como el conjunto de todos los puntos en \(A\) que no están en \(B\).

Las operaciones de complemento, unión e intersección de conjuntos se han introducido en las definiciones Definición 1.4 a Definición 1.6, respectivamente. Estas operaciones de conjuntos satisfacen varias leyes, que a continuación se sintetizan. (Ash y Doleans-Dade 2000)

Teorema 1.1 (Leyes del álgebra de conjuntos)  

  1. Leyes de idempotencia \[\begin{split}A\cup A &= A \\A\cap A &=A\end{split}\]
  2. Leyes asociativas \[\begin{split} (A\cup B)\cup C &= A \cup (B\cup C)\\ (A\cap B)\cap C &= A\cap (B \cap C)\end{split}\]
  3. Leyes conmutativas \[\begin{split} A\cup B &= B\cup A\\ A\cap B &= B \cap A \end{split}\]
  4. Leyes distributivas \[\begin{split} A\cup (B\cap C) &= (A\cup B)\cap (A\cup C)\\ A\cap (B\cup C) &= (A\cap B)\cup (A\cap C) \end{split} \]
  5. Leyes de identidad \[\begin{split} A\cup \emptyset &= A\\ A\cap \Omega &= A\\ A\cup \Omega &= \Omega\\ A\cap \emptyset &= \emptyset \end{split} \]
  6. Leyes de complemento \[\begin{split} A\cup A^c &= \Omega\\ A\cap A^c &= \emptyset\\ (A^c)^c &= A\\ \Omega^c&=\emptyset\\ \emptyset^c&= \Omega \end{split} \]
  7. Leyes de De Morgan \[\begin{split} (A\cup B)^c &=A^c \cap B^c\\ (A\cap B)^c &=A^c \cup B^c \end{split} \]
Figura 1.1: Diagramas de Venn

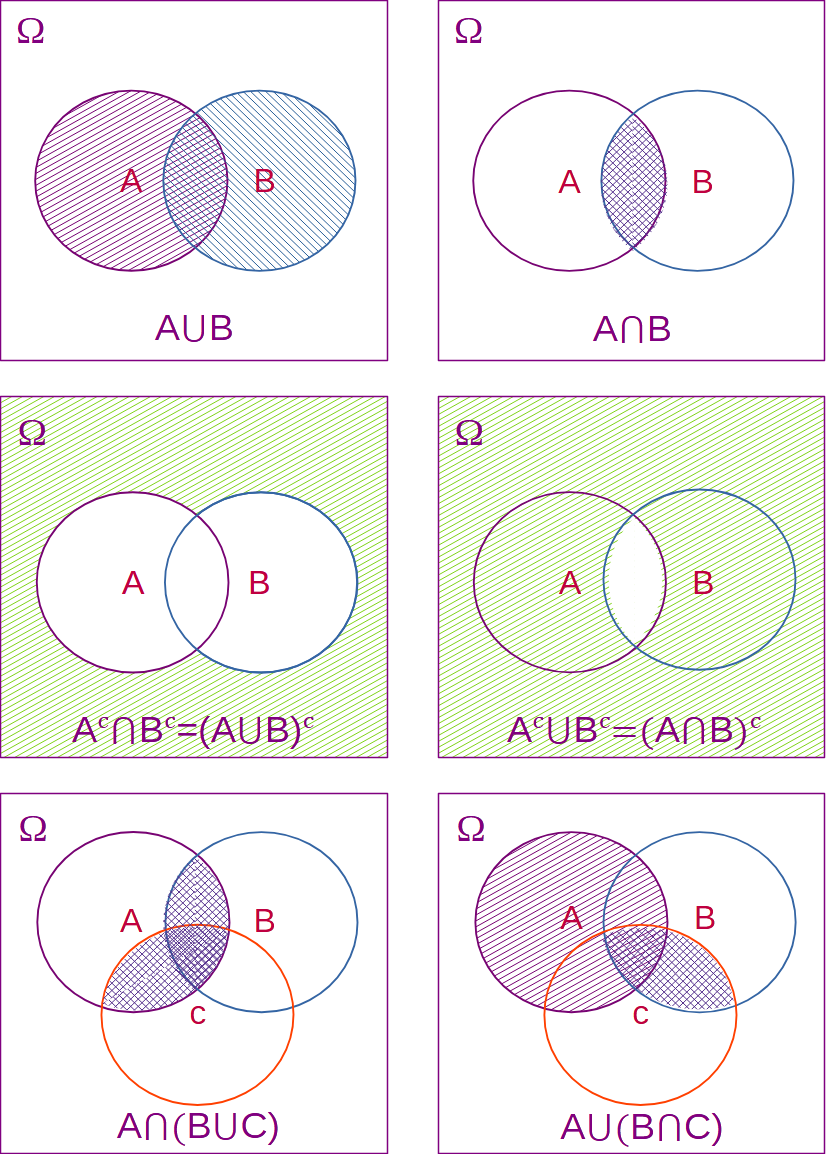
Algunas de las leyes del álgebra de conjuntos se ilustran en los diagramas de Venn en la Figura 1.1. Aunque se utilizará libremente cualquiera de las leyes mencionadas, podría resultar instructivo proporcionar una prueba de una de ellas para ilustrar la técnica. Se considera el siguiente ejemplo:

Demostrar que \((A \cup B)^c = A^c \cap B^c\).

Prueba. Según la definición, dos conjuntos son iguales si cada uno está contenido en el otro. Primero se demuestra que \((A\cup B)^c \subset A^c\cap B^c\) al probar que si \(\omega \in (A\cup B)^c\), entonces \(\omega \in A^c \cap B^c\). Ahora bien, \(\omega \in (A\cup B)^c\) implica que \(\omega \notin A \cup B\), lo cual implica que \(\omega \notin A\) y \(\omega \notin B\), lo que a su vez implica que \(\omega \in A^c\) y \(\omega \in B^c\); es decir, \(\omega \in A^c\cap B^c\). A continuación se demuestra que \(A^c \cap B^c \subset (A\cup B)^c\). Sea \(\omega \in A^c \cap B^c\), lo que significa que \(\omega\) pertenece tanto a \(A^c\) como a \(B^c\). Entonces, \(\omega \notin A \cup B\), ya que de lo contrario \(\omega\) debería pertenecer al menos a uno de los conjuntos \(A\) o \(B\), lo cual contradice que \(\omega\) pertenezca tanto a \(A^c\) como a \(B^c\); sin embargo, \(\omega \notin A \cup B\) implica que \(\omega \in (A\cup B)^c\), lo que completa la prueba.

Se han introducido la unión y la intersección de dos conjuntos; estas definiciones se extienden inmediatamente a más de dos conjuntos, de hecho, a un número arbitrario de conjuntos. Es costumbre distinguir entre los conjuntos en una colección de subconjuntos de \(\Omega\) asignándoles nombres en forma de subíndices.

Se considera el conjunto de índices \(\Lambda\) como el catálogo de nombres o índices. A \(\Lambda\) también se le denomina conjunto de índices. Por ejemplo, si se tiene interés únicamente en dos conjuntos, entonces el conjunto de índices \(\Lambda\) incluye solo dos índices, por ejemplo, 1 y 2; así, \(\Lambda=\{1,2\}\).

Definición 1.8 (Unión e intersección de conjuntos) Sea \(\Lambda\) un conjunto de índices y \(\{A_\lambda: \lambda \in \Lambda\}= \{A_\lambda\}\), una colección de subconjuntos de \(\Omega\) indexados por \(\Lambda\). El conjunto de puntos que consiste en todos los puntos que pertenecen a \(A_\lambda\) para al menos un \(\lambda\) se denomina unión de los conjuntos \(\{A_\lambda\}\) y se denota como \(\bigcup\limits_{\lambda\in \Lambda} A_\lambda\). El conjunto de puntos que consiste en todos los puntos que pertenecen a \(A_\lambda\) para cada \(\lambda\) se denomina intersección de los conjuntos \(\{A_\lambda\}\) y se denota como \(\bigcap\limits_{\lambda\in\Lambda} A_\lambda\). Si \(\Lambda\) está vacío, entonces se define \(\bigcup\limits_{\lambda\in \Lambda} A_\lambda = \emptyset\) y \(\bigcap\limits_{\lambda\in\Lambda} A_\lambda=\Omega\).

Uno de los teoremas fundamentales que relaciona las uniones, intersecciones y complementos para una colección arbitraria de conjuntos se debe a De Morgan.

Teorema 1.2 (Teorema de De Morgan) Sea \(\Lambda\) un conjunto de índices y \(\{A_\lambda\}\) una colección de subconjuntos de \(\Omega\) indexados por \(\Lambda\). Entonces,

  1. \(\left(\bigcup\limits_{\lambda\in\Lambda} A_\lambda\right)^c = \bigcap\limits_{\lambda\in\Lambda} A_\lambda^c\)

  2. \(\left(\bigcap\limits_{\lambda\in\Lambda} A_\lambda\right)^c = \bigcup\limits_{\lambda\in\Lambda} A_\lambda^c\)

Definición 1.9 (Disjuntos o mutuamente excluyentes) Los subconjuntos \(A\) y \(B\) de \(\Omega\) se definen como mutuamente excluyentes o disjuntos si \(A\cap B=\emptyset\). Los subconjuntos \(A_1, A_2, \ldots\) se definen como mutuamente excluyentes si \(A_i\cap A_j=\emptyset\) para cada \(i\neq j\).