6 Redes Neuronales
El funcionamiento de los cerebros de humanos y otros animales es intrigante porque son capaces de realizar tareas muy complejas en un tiempo muy corto y con alta eficiencia. Por ejemplo, las señales de los sensores en el cuerpo transmiten información relacionada con la vista, el oído, el gusto, el olfato, el tacto, el equilibrio, la temperatura, el dolor, etc. Luego, las neuronas del cerebro, que son unidades autónomas, transmiten, procesan y almacenan esta información para que se pueda responder con éxito a estímulos externos e internos. Las neuronas de muchos animales transmiten picos de actividad eléctrica a través de una hebra larga y delgada llamada axón. Un axón se divide en miles de terminales o ramas, donde, según el tamaño de la señal, se conectan a dendritas de otras neuronas (Figura 6.1). Se estima que el cerebro está compuesto por alrededor de \(10^{11}\) neuronas que trabajan en paralelo, ya que el procesamiento realizado por las neuronas y la memoria capturada por las sinapsis se distribuyen juntas sobre la red. La cantidad de información procesada y almacenada depende de los niveles umbral de disparo y también del peso dado por cada neurona a cada una de sus entradas. Una de las características de las neuronas biológicas, a las que deben su gran capacidad para procesar y realizar tareas altamente complejas, es que están altamente conectadas con otras neuronas de las cuales reciben estímulos de un evento a medida que ocurre, o cientos de señales eléctricas con la información aprendida.
Las redes neuronales tienen sus raíces en la búsqueda de emular el funcionamiento del cerebro humano en la década de 1940. McCulloch y Pitts (1943) propusieron el concepto inicial de una “neurona artificial” que podría realizar operaciones lógicas básicas. Sin embargo, fue en la década de 1950 cuando el psicólogo Frank Rosenblatt desarrolló el “perceptrón”, Rosenblatt (1960), un tipo de red neuronal que podía aprender a reconocer patrones a través de entrenamiento.
A pesar de su potencial, las limitaciones del perceptrón y la falta de avances en la capacidad computacional llevaron a un declive en la investigación en redes neuronales en los años siguientes. Sin embargo, en la década de 1980 y 1990, hubo un resurgimiento del interés debido a nuevos algoritmos de aprendizaje y avances en el hardware, permitiendo el entrenamiento de redes más complejas.
La importancia de las redes neuronales en la predicción de datos radica en su capacidad para aprender patrones y relaciones en conjuntos de datos vastos y complejos. A través del proceso de entrenamiento, una red neuronal ajusta sus pesos y conexiones internas para capturar características relevantes en los datos. Esto les permite realizar tareas como clasificación y regresión, lo que a su vez permite la predicción de resultados futuros.
Con el tiempo, las redes neuronales se han vuelto más sofisticadas, dando lugar a arquitecturas como las redes neuronales convolucionales (CNN) para el procesamiento de imágenes y las redes neuronales recurrentes (RNN) para el procesamiento de secuencias. Además, el surgimiento del aprendizaje profundo (deep learning) ha permitido el entrenamiento de redes neuronales con muchas capas, lo que ha mejorado significativamente su capacidad para abordar problemas complejos de predicción.
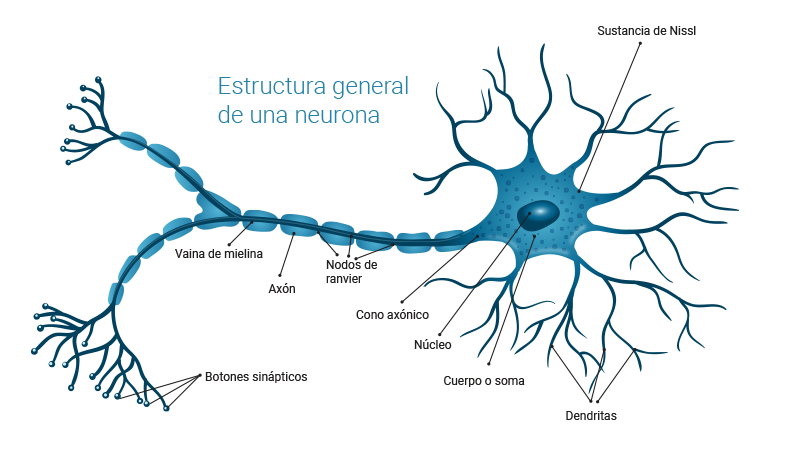
6.1 Elementos fundamentales de las Redes Neuronales Artificiales
Para obtener una comprensión clara de los principales elementos utilizados para construir modelos de redes neuronales artificiales (RNA), en la Figura 6.2 se presenta un modelo general de red neuronal artificial que incorpora los componentes fundamentales para este tipo de modelos.
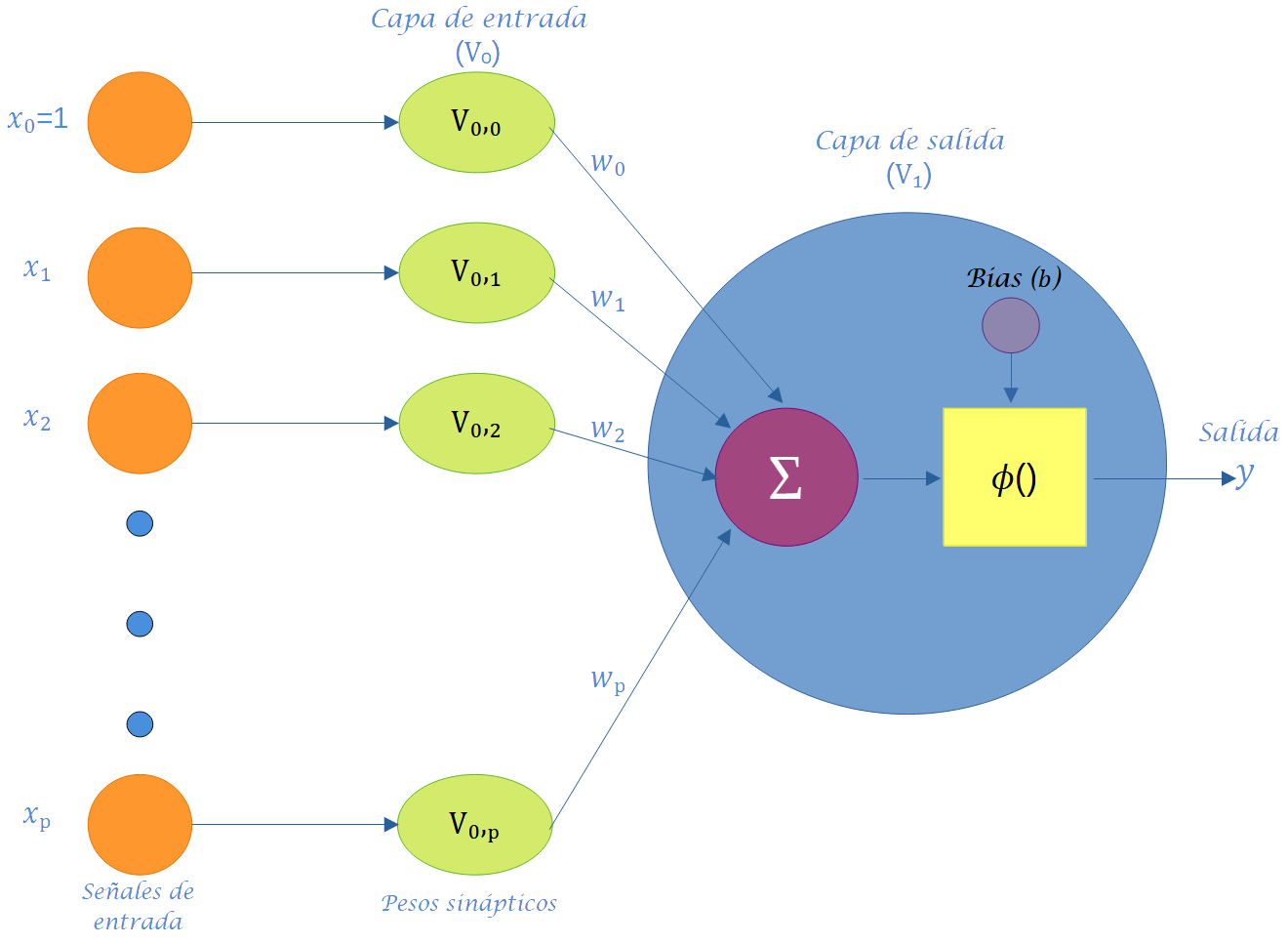
La información de entrada, \(x_1, ..., x_p\), es recibida por la neurona del sistema sensorial externo u otras neuronas con las que tiene conexión. El vector de pesos sinápticos \(\mathbf{w} = (w_1, ..., w_p)\) modifica la información recibida emulando la sinapsis entre las neuronas biológicas. Estos pueden interpretarse como ganancias que pueden atenuar o amplificar los valores que desean propagar hacia la neurona. El parámetro \(b_j\) se conoce como el sesgo (intercepto o umbral) de una neurona. En redes neuronales artificiales, el aprendizaje se refiere al método de modificar los pesos de las conexiones entre los nodos (neuronas) de una red especificada.
Los valores recibidos por la neurona son ajustados por los pesos sinápticos y sumados para generar la entrada neta, expresada matemáticamente como:
\[v_j=\sum_{j=1}^p \omega_{ij}x_j.\]
La entrada neta \((v_j)\) determina si la neurona se activa o no. La activación de la neurona depende de la función de activación, evaluándose la entrada neta en dicha función para obtener la salida de la red;
\[ y_j=g(v_j), \]
donde \(g\) representa la función de activación. Por ejemplo, si se define esta función como un escalón unitario (también llamado umbral), la salida será \(1\) si la entrada neta es mayor que cero; de lo contrario, la salida será \(0\).
Aunque no existe un comportamiento biológico análogo a las neuronas cerebrales, el uso de la función de activación es un artificio que permite aplicar RNA a una variedad de problemas reales. La salida \(y_j\) de la neurona se genera al evaluar la entrada neta \((v_j)\) en la función de activación, pudiendo propagarse a otras neuronas o ser la salida final de la red, con una interpretación específica según la aplicación.
En términos generales, el funcionamiento de un modelo de red neuronal artificial se lleva a cabo mediante elementos simples denominados neuronas. Las señales se transmiten entre neuronas a través de enlaces de conexión, cada uno con un peso asociado que multiplica la señal transmitida. Cada neurona aplica una función de activación (generalmente no lineal) a las entradas de la red (suma ponderada de las señales de entrada) para determinar su signo correspondiente.
Un modelo de RNA de una sola capa, como el presentado en la Figura 6.2, posee una capacidad de procesamiento limitada por sí mismo y una aplicabilidad reducida; su verdadero poder radica en la interconexión de múltiples redes neuronales artificiales, similiar al funcionamiento del cerebro humano. Este enfoque ha motivado a diversos investigadores a proponer diversas arquitecturas para la interconexión de neuronas en el contexto de RNA. A continuación, se presentan las definiciones de RNA y aprendizaje profundo (Montesinos López, Montesinos López, y Crossa (2022)).
Definición 6.1 (Red Neuronal Artificial) Una red neuronal artificial es un sistema compuesto por numerosos elementos de procesamiento simples que operan en paralelo, y cuya función está determinada por la estructura de la red y el peso de las conexiones. En cada uno de los nodos o elementos de cómputo, que posee una capacidad de procesamiento baja, se lleva a cabo el procesamiento.
Definición 6.2 (Aprendizaje profundo) Se define el aprendizaje profundo como una generalización de RNA donde se utilizan más de una capa oculta, lo que implica que se utilizan más neuronas para implementar el modelo. Por esta razón, a una red neuronal artificial con múltiples capas ocultas se le llama Red Neuronal Profunda (RNP) y la práctica de entrenar este tipo de redes se llama aprendizaje profundo (AP).
Para una comprensión más completa de los elementos que componen una red neuronal artificial, resulta crucial diferenciar entre las diversas categorías de capas y tipos de neuronas. Por consiguiente, se procede a detallar los tipos de capas seguido por una exposición más detallada de los tipos de neuronas.
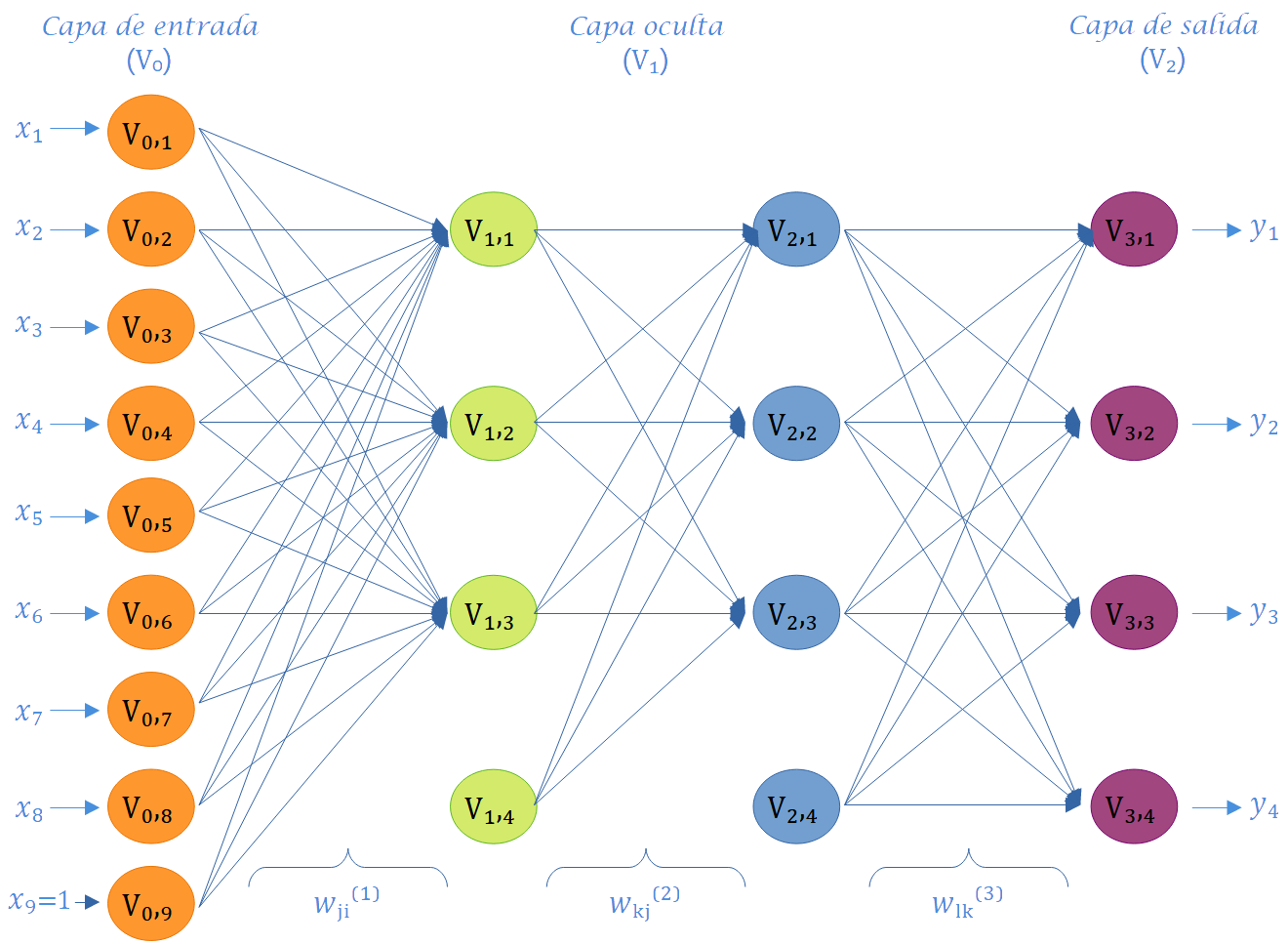
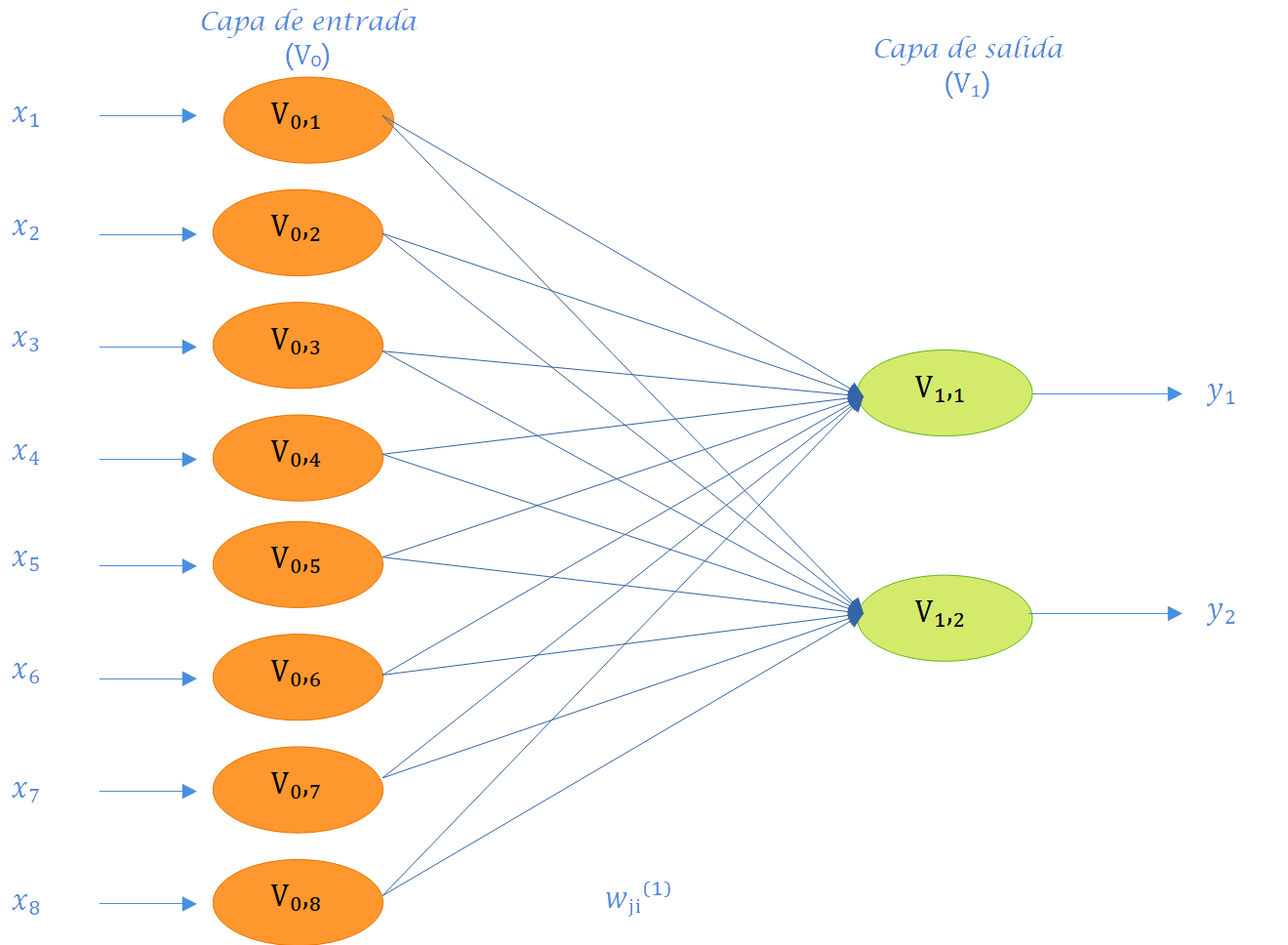
Capa de entrada: Es el conjunto de neuronas que recibe directamente la información proveniente de las fuentes externas de la red. En el contexto de la Figura 6.3, esta información es \(x_1, ... ,x_8\). Por lo tanto, el número de neuronas en una capa de entrada es la mayoría de las veces igual al número de variables explicativas de entrada proporcionadas a la red. Por lo general, las capas de entrada están seguidas por al menos una capa oculta. Solo en las redes neuronales feedforward, las capas de entrada están completamente conectadas a la siguiente capa oculta.
Capas ocultas: Consisten en un conjunto de neuronas internas de la red que no tienen contacto directo con el exterior. El número de capas ocultas puede ser \(0, 1\) o más. En general, las neuronas de cada capa oculta comparten el mismo tipo de información; por esta razón, se llaman capas ocultas. Las neuronas de las capas ocultas pueden estar interconectadas de diferentes maneras; esto determina, junto con su número, las diferentes arquitecturas de RNA y RNP. La información aprendida extraída de los datos de entrenamiento se almacena y captura mediante los valores de peso de las conexiones entre las capas de la red neuronal artificial. Además, es importante señalar que las capas ocultas son componentes clave para capturar de manera más eficiente comportamientos no lineales complejos de los datos.
Capa de salida: Es un conjunto de neuronas que transfiere la información procesada por la red hacia el exterior. En la Figura 6.3, las neuronas de salida corresponden a las variables de salida \(y_1, y_2, y_3\) e \(y_4\). Esto implica que la capa de salida proporciona la respuesta o predicción del modelo de red neuronal artificial basada en la entrada proveniente de la capa de entrada. La salida final puede ser continua, binaria, ordinal o de conteo, dependiendo de la configuración de la RNA, la cual está controlada por la función de activación especificada en las neuronas de la capa de salida.
A continuación, se definen los tipos de neuronas:
Neurona de entrada: Una neurona que recibe entradas externas desde fuera de la red.
Neurona de salida: Una neurona que produce algunas de las salidas de la red.
Neurona oculta: Una neurona que no tiene interacción directa con el “mundo exterior” sino solo con otras neuronas dentro de la red. Una terminología similar se utiliza a nivel de capa para redes neuronales multicapa.
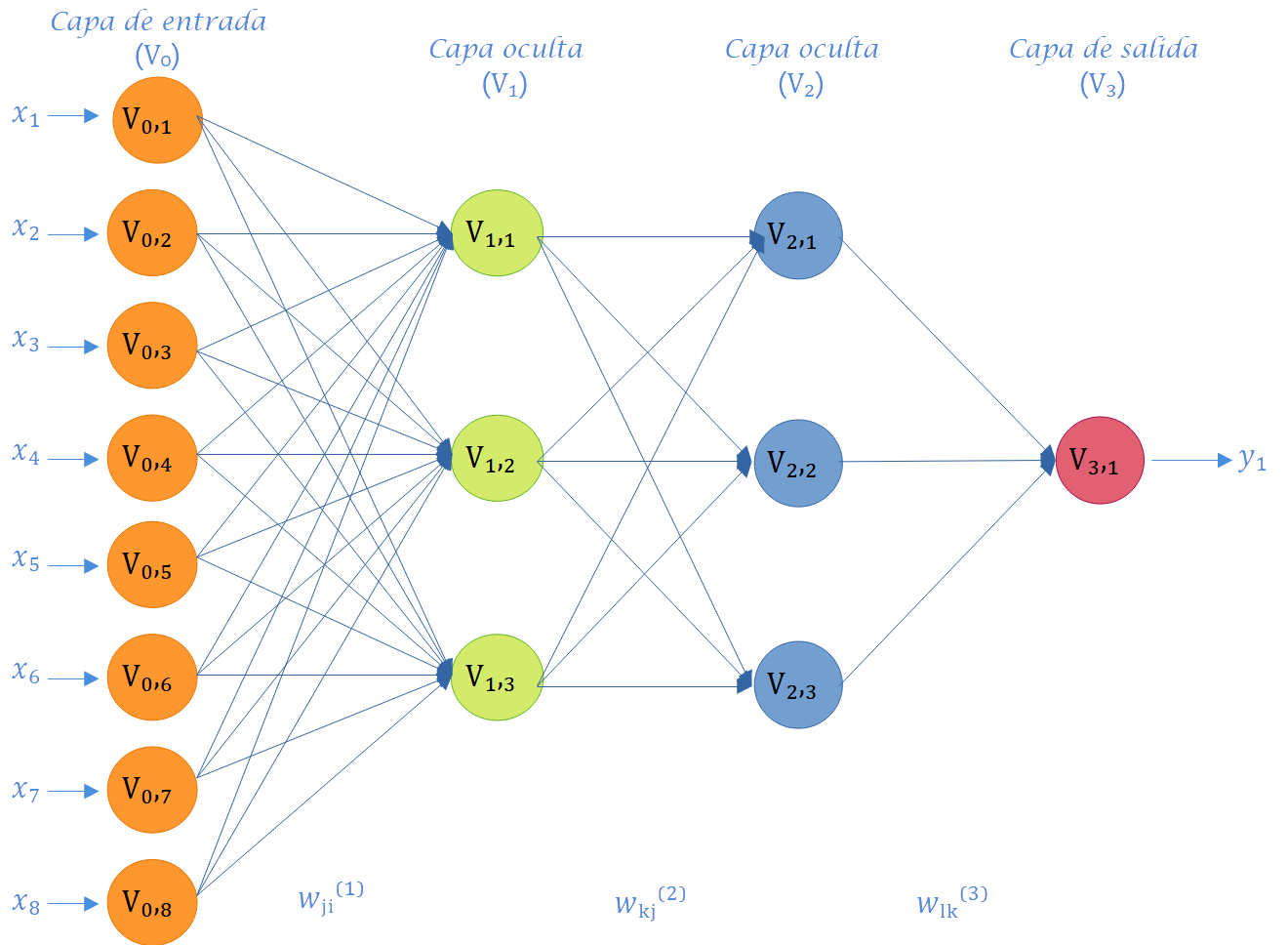
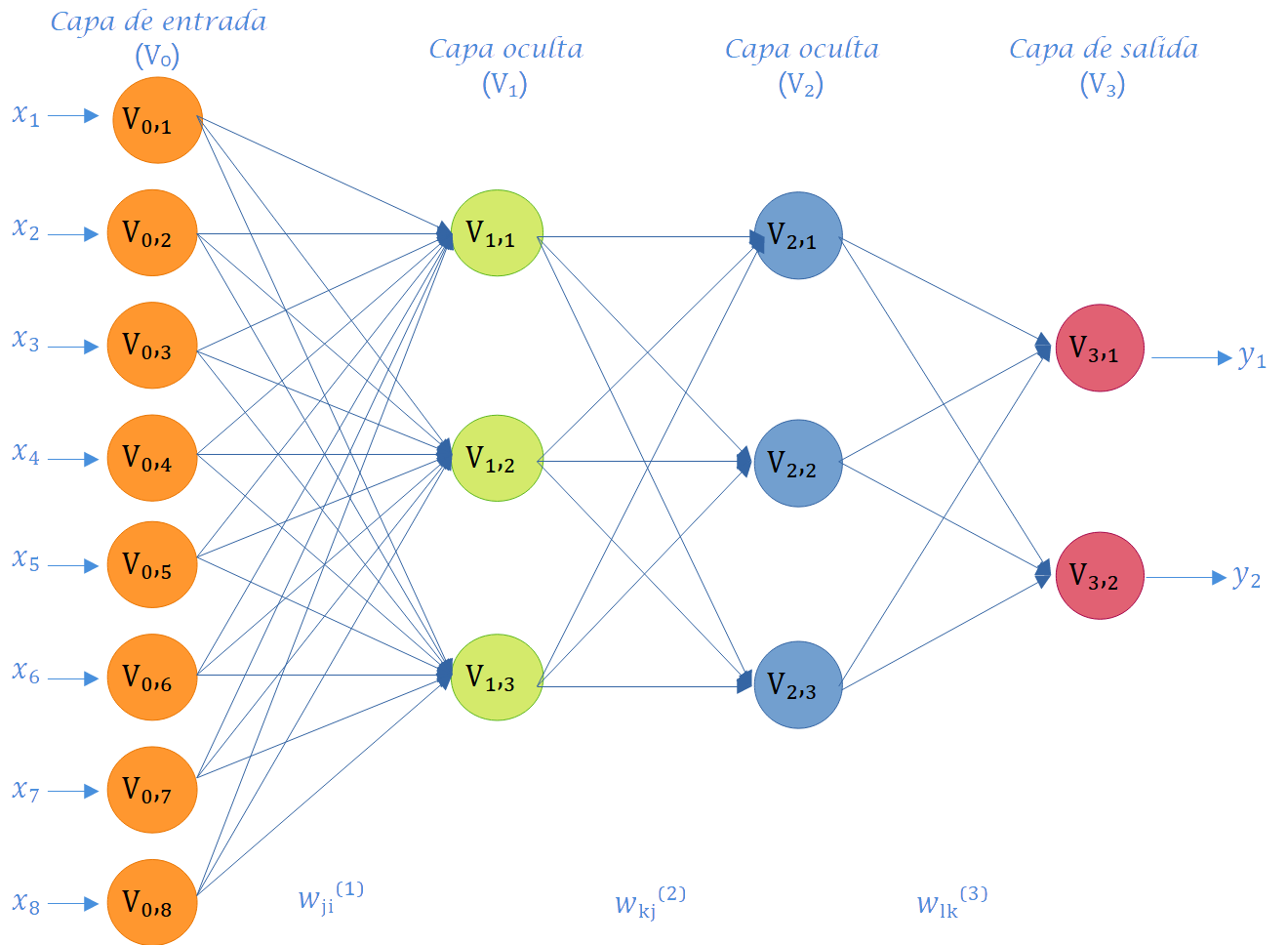
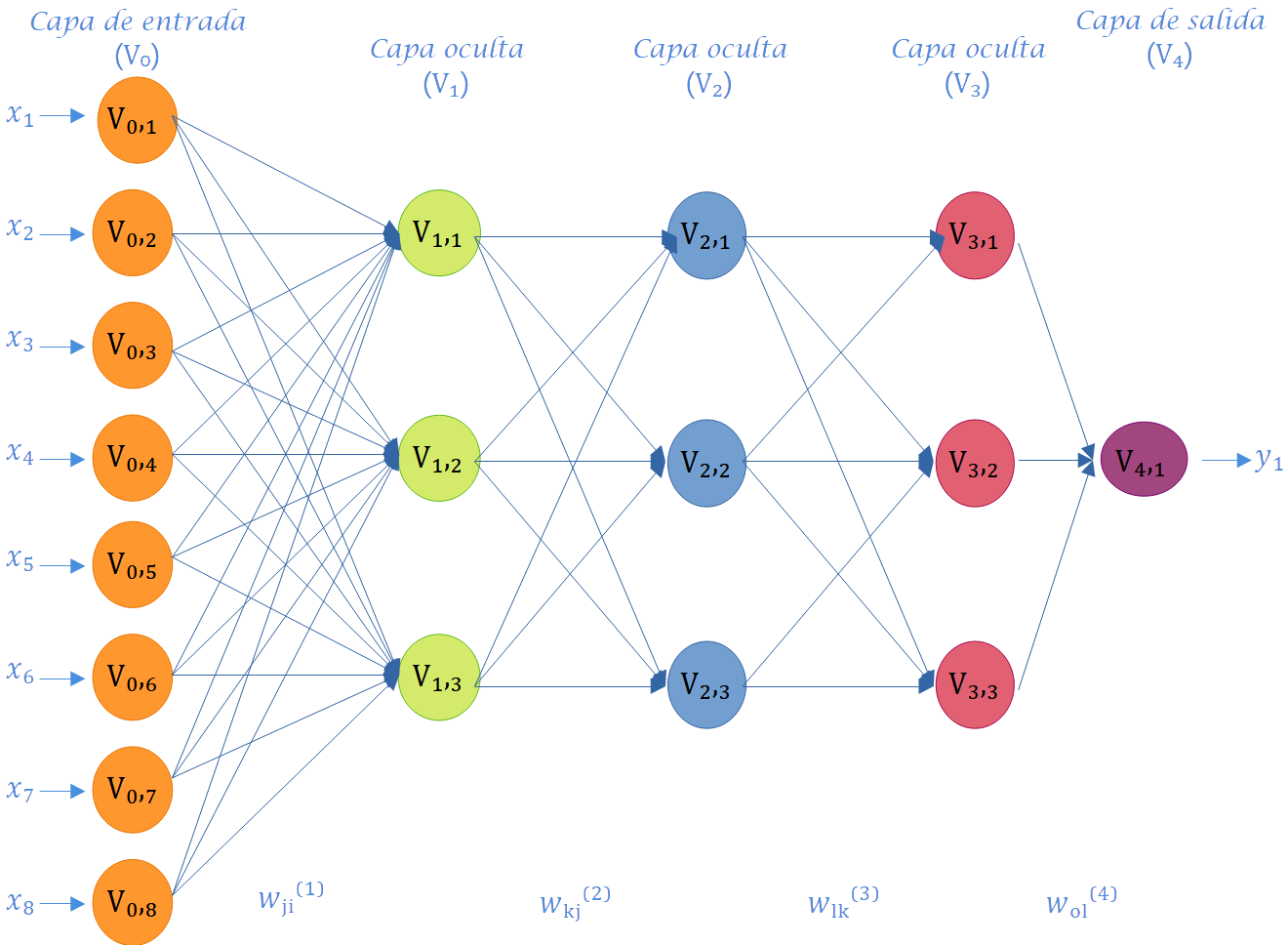
Como se aprecia en la Figura 6.3, la disposición de las neuronas en una red neuronal artificial se lleva a cabo mediante la formación de niveles que contienen un número específico de neuronas. Cuando un conjunto de neuronas artificiales recibe simultáneamente el mismo tipo de información, se le denomina capa. Además, se hace referencia a una red compuesta por tres tipos de niveles como capas. La Figura 6.4 exhibe otras seis redes con diversos números de capas, y la mitad de ellas (Figura 6.4 (a), Figura 6.4 (c), Figura 6.4 (e)) son univariadas, ya que la variable de respuesta a predecir es única, mientras que la otra mitad (Figura 6.4 (b), Figura 6.4 (d), Figura 6.4 (f)) son multivariadas, dado que la red tiene el propósito de predecir dos salidas. Es relevante destacar que los paneles a y b en la Figura 6.4 representan redes con solo una capa y sin capas ocultas; por consiguiente, este tipo de redes corresponde a modelos convencionales de regresión o clasificación por regresión.
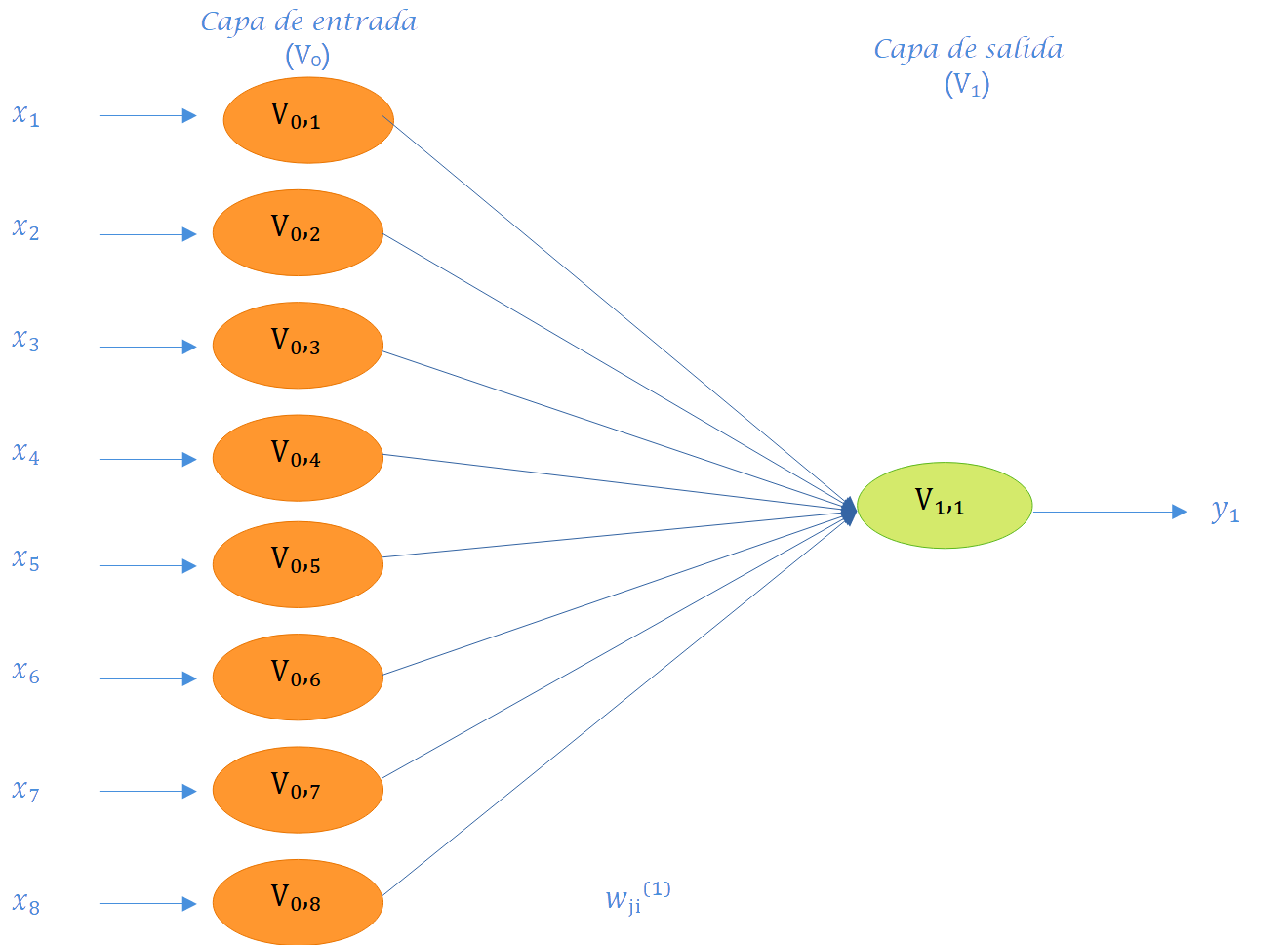
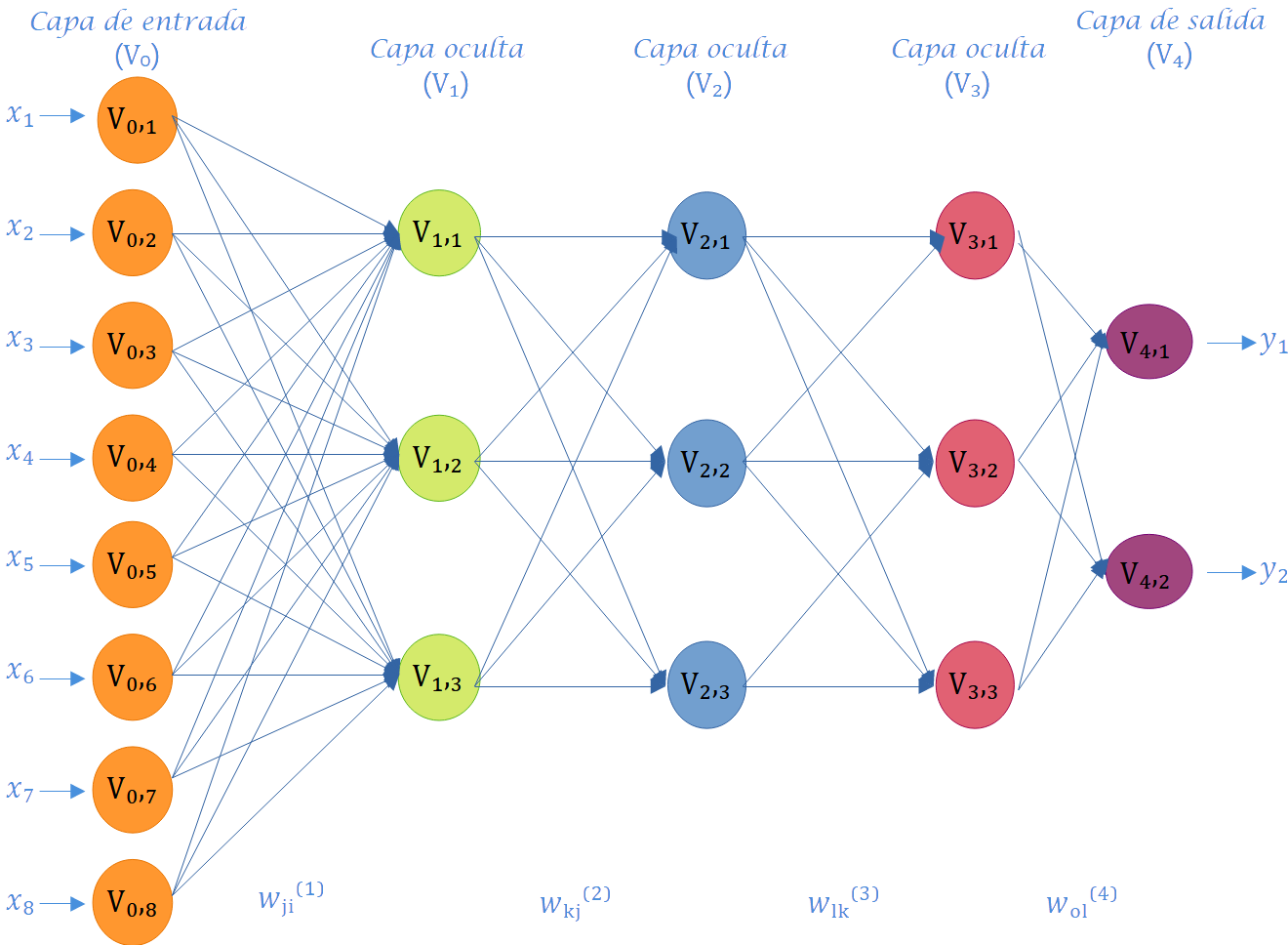
En consecuencia, la arquitectura de una red neuronal artificial se refiere a la manera en que las neuronas están organizadas en la red, y está estrechamente vinculada al algoritmo de aprendizaje empleado para entrenar la red. Según el número de capas, clasificamos las redes como monocapa o multicapa; y si consideramos la dirección del flujo de información como criterio clasificatorio, las redes se denominan de avance o recurrentes. Cada tipo de arquitectura se aborda la siguiente sección.
6.2 Arquitectura
6.2.1 Perceptrón simple
El perceptrón simple consta de cuatro componentes fundamentales en su estructura. Estos son: las entradas (input) con conexiones y pesos (nodos ponderados), el nodo de procesamiento o suma, la función de activación y las salidas (output). El nodo de procesamiento realiza una regresión lineal, involucrando la suma ponderada de los pesos en cada nodo de las entradas y un término de sesgo o término independiente. En esencia, el perceptrón simple funciona como un discriminador lineal que, a partir de un umbral establecido, produce una salida binaria.
Desde una perspectiva matemática, el perceptrón simple se representa mediante la siguiente ecuación:
\[ \hat{\mathbf{y}}(\mathbf x)=f(\mathbf w^T\mathbf x+b). \tag{6.1}\]
La arquitectura que modela esta ecuación se describe a través de la Figura 6.5,
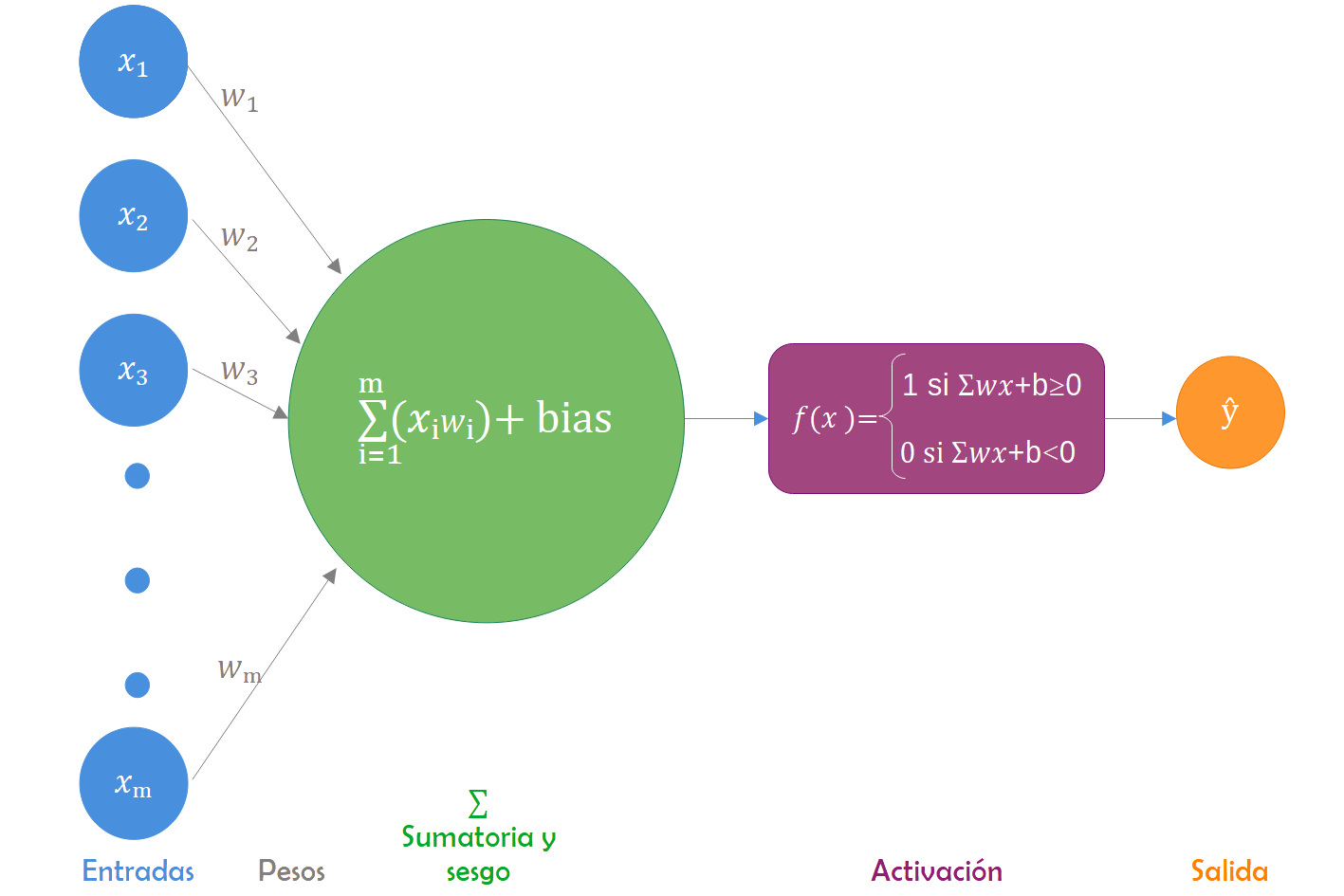
donde \(\mathbf x\) denota el vector de entradas, \(\mathbf w\) denota el vector de pesos asociados a cada nodo, \(b\) denota el sesgo o intercepto de la regresión, \(\sum\) denota el nodo de procesamiento o combinador lineal y \(f\) denota la función de activación o función limitadora, siendo esta última una transformación no lineal de la regresión obtenida en el nodo de procesamiento.
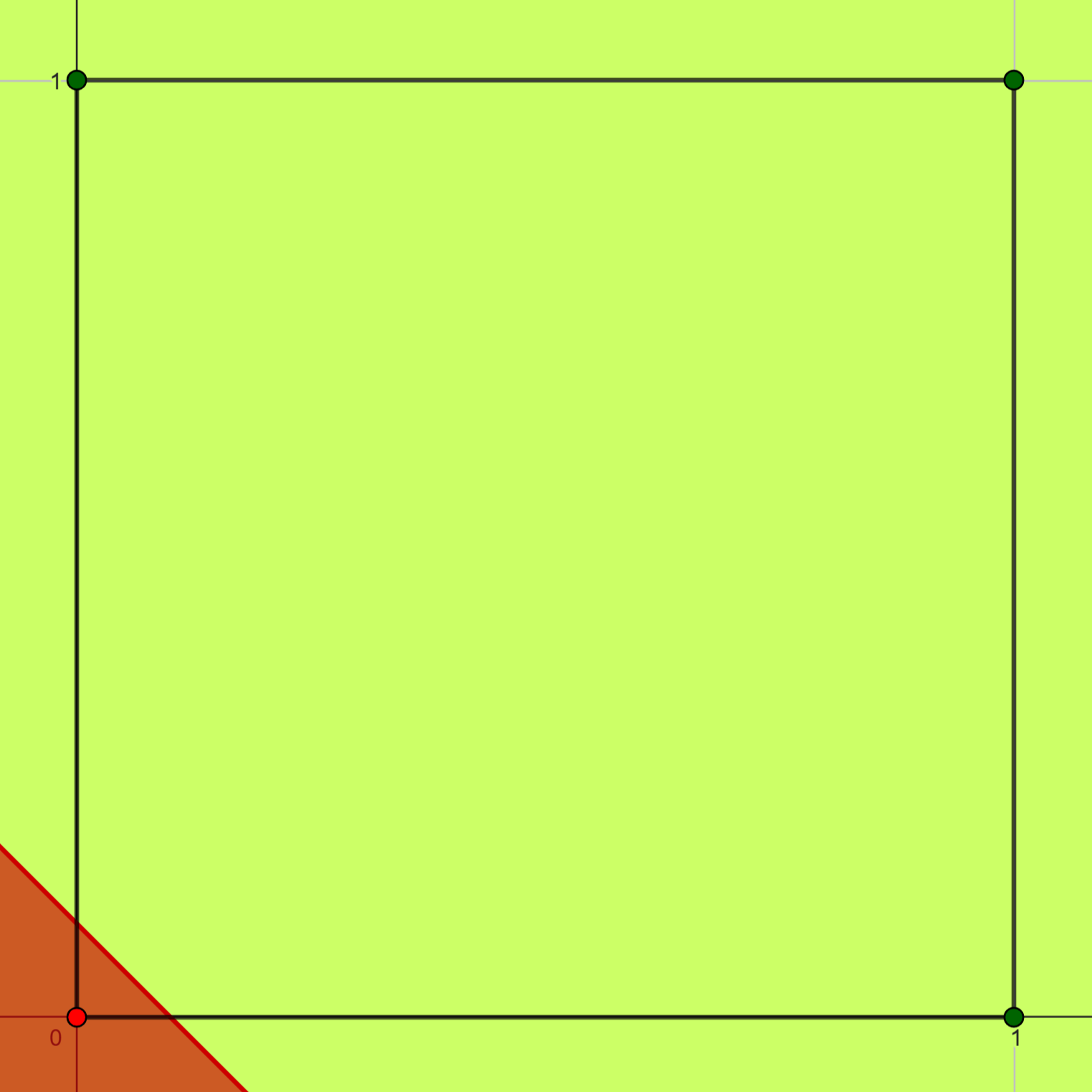
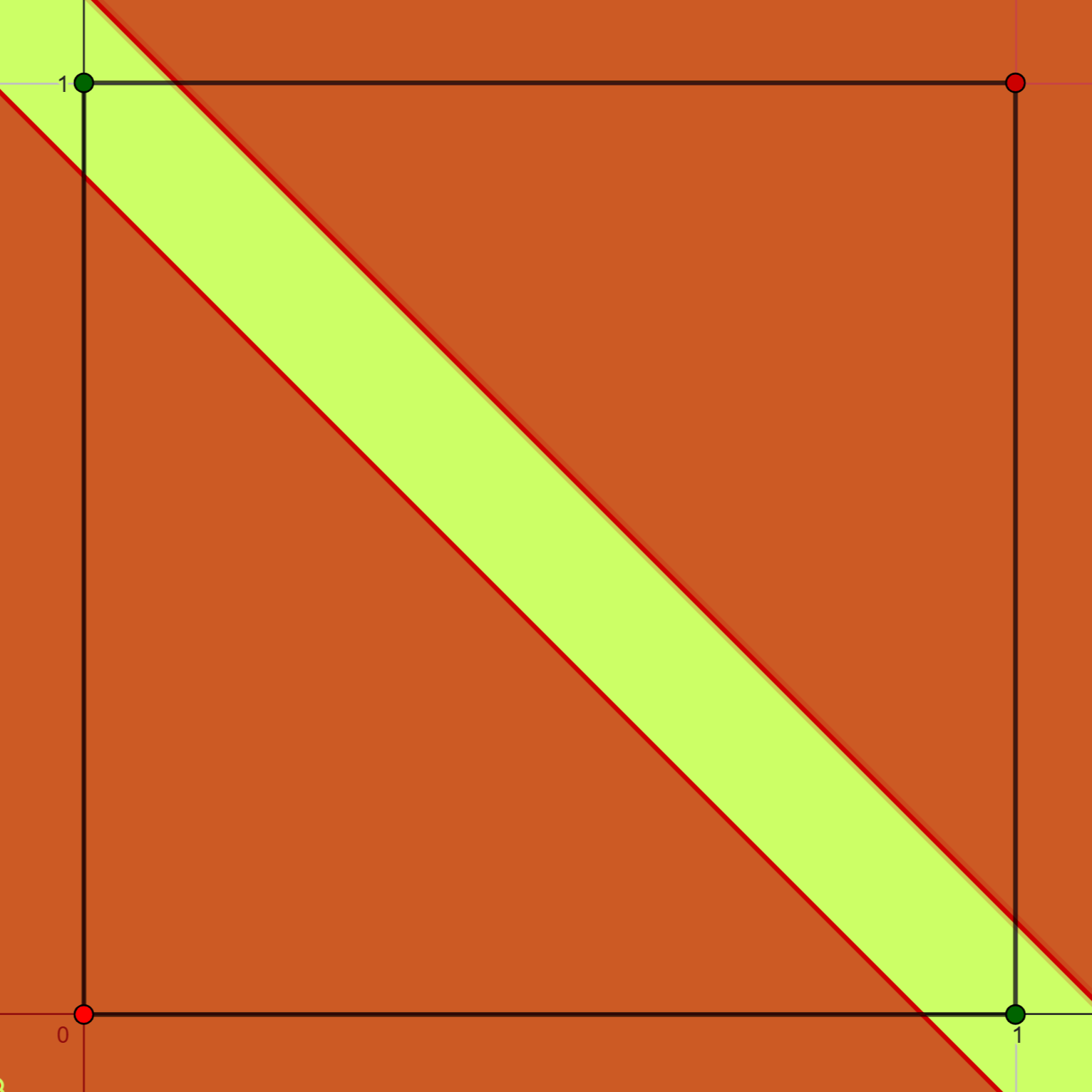
Aunque el perceptrón simple demuestra eficacia en el aprendizaje y la resolución de problemas linealmente separables, como las compuertas lógicas AND (Figura 6.6 (b)) y OR (Figura 6.6 (a)) , presenta limitaciones en la resolución de problemas que no son de este tipo. Un ejemplo paradigmático de ello es su incapacidad para clasificar las salidas de una compuerta lógica del tipo XOR (Figura 6.6 (c)), ya que el nodo de procesamiento solo permite la separación de la información mediante una única recta de regresión.

6.2.2 Perceptrón Multicapa (MLP)
La solución al problema de la puerta lógica XOR consiste en la adición de una neurona adicional, permitiendo así la definición de una nueva recta de regresión, como se ilustra en la Figura 6.6 (c). Esto conduce a la creación de lo que se conoce como Perceptrón Multicapa o MLP (por sus siglas en inglés), también reconocido como Red Neuronal Profunda. Esta estructura representa una generalización del perceptrón simple, incorporando más de un nivel de neuronas y/o una o varias capas de neuronas “entre” la capa de entradas y la capa de salidas, las cuales son denominadas capas ocultas. En estas capas ocultas, las funciones de activación entre las neuronas no son necesariamente lineales. Las MLP son consideradas las redes neuronales artificiales por defecto y se representan mediante un diagrama simple, que transmite las entradas de capa en capa hasta alcanzar la capa final.
La red neuronal de la Figura 8.11 ejemplifica un MLP de dos capas ocultas. En esta representación, los superíndices indican la posición en las capas, mientras que los subíndices indican la posición relativa de cada nodo en su respectiva capa. La red consta de un vector de entradas \(\mathbf{x} \in \mathbb{R}^{d_0}\), donde \(\mathbf{x} = (x_1, \ldots, x_{d_0})^T\), capas ocultas denotadas por \(a^l\), y un vector de salidas \(\hat{y} \in \mathbb{R}^{d_L}\) con \(\hat{y} = (\hat{y}_1, \ldots,\hat y_{d_L})^T\). Las capas ocultas contienen nodos de procesamiento o neuronas representadas por \(a = f(z)\), donde \(f\) es la función de activación de cada capa y \(z\) es un combinador lineal (matricial). Las conexiones entre las capas están ponderadas por \(\mathbf{w}\), que representa las matrices de pesos asociadas en cada capa. Por ejemplo, \(w_{ij}^1\) representa el peso asociado a la conexión entre la entrada j-ésima y el i-ésimo nodo de procesamiento en la primera capa oculta. Las matrices \(\mathbf{w}^l\) tienen dimensiones \((d_l \times d_{l-1})\), donde la capa de entrada se considera como capa cero \((l = 0)\).
Es importante destacar que el término \(b\), que indica el sesgo en el perceptrón simple, también se incluye en la red MLP en cada nodo de procesamiento, específicamente en el combinador lineal \(z\). A partir de este momento, el nodo de procesamiento incorporará el término de sesgo \(b\), y \(b^1 \in a^1\) denotará el vector de sesgo en la primera capa oculta.
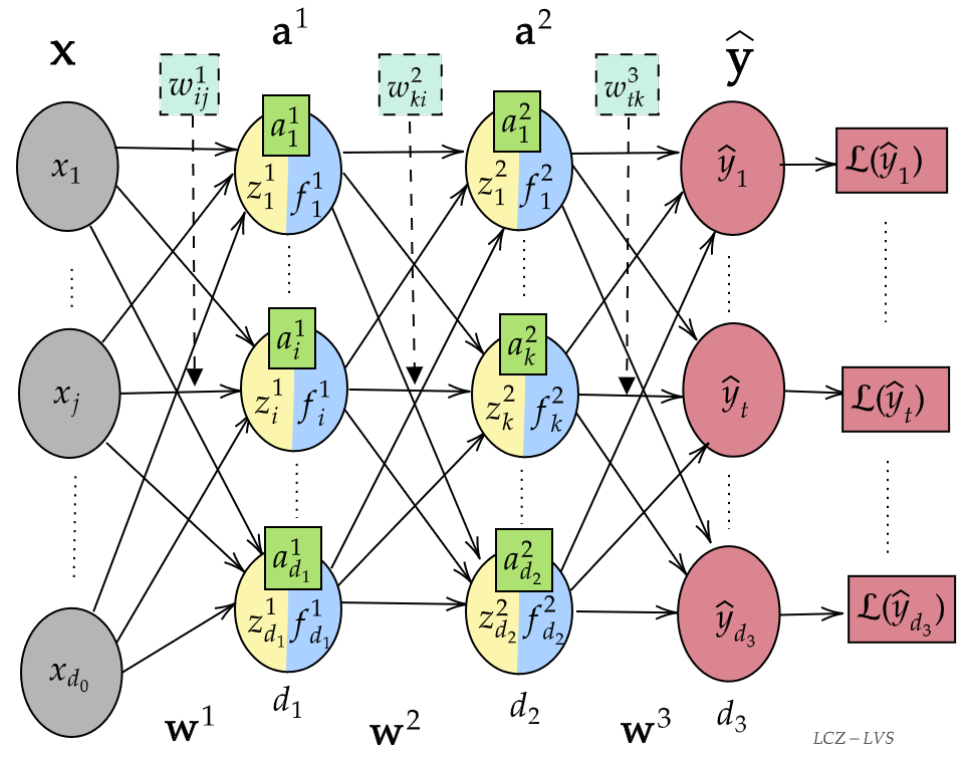
La ecuación matemática que describe la red de la Figura 8.11 es la siguiente:
\[ \begin{split}\hat{\mathbf{y}} &= f^3(z^3) \\&= f^3(\mathbf{w}^3 a^2 + b^3) \\&= f^3(\mathbf{w}^3 (f^2(z^2)) + b^3) \\&= f^3(\mathbf{w}^3 (f^2(\mathbf{w}^2 a^1 + b^2)) + b^3) \\&= f^3(\mathbf{w}^3 (f^2(\mathbf{w}^2 (f^1(z^1)) + b^2)) + b^3) \\&= f^3(\mathbf{w}^3 (f^2(\mathbf{w}^2 (f^1(\mathbf{w}^1 \mathbf{x} + b^1)) + b^2)) + b^3).\end{split} \]
Se observa que \(f^3\) representa la función de activación en la capa de salida, la cual comúnmente se elige como la identidad. Sin embargo, en algunos modelos de clasificación, la predicción puede ser más precisa si esta función es no lineal y limitadora.
Por otro lado, la última columna en la Figura 8.11 constituye una capa adicional en la cual, a través de una función de pérdida, se evalúa el rendimiento de la red. Esta evaluación relaciona la información obtenida en la capa de salida con los datos esperados en un modelo de aprendizaje supervisado.
6.3 Perceptrón
En un principio, se establece un conjunto de datos a estudiar denominado \(\mathbf X \subseteq \mathbb R^{m+1}\). Este conjunto se particiona en dos clases linealmente separables, \(\mathscr C_1\) y \(\mathscr C_2\). A los vectores \(\mathbf x = (x_1, x_2,...,x_m,1)^T\) que pertenecen a \(\mathbf X\), se les denomina entradas.
A continuación, se introduce un conjunto \(\mathbf W \subseteq \mathbb R^{m+1}\), que contiene etiquetas para los nodos del perceptrón. Los elementos de este conjunto, denotados como \(\mathbf w = (w_1,w_2,...,w_m,b)^T\), se llaman pesos sinápticos. Aquí, \(b\) es un número real fijo conocido como sesgo. Con el propósito de describir el algoritmo del Perceptrón, se presentan cuatro definiciones fundamentales:
Definición 6.3 (Clases linealmente separables) Sean \(\mathscr C_1\) y \(\mathscr C_2\) dos clases en un espacio \(n-\)dimensional. \(\mathscr C_1\) y \(\mathscr C_2\) se consideran clases linealmente separables si existe un vector \(\mathbf w \in \mathbb R^{m+1}\) de pesos sinápticos que cumple con las siguientes condiciones: \[ \begin{split} \mathbf w^T \mathbf x_1 &> 0\text{ para cada vector de entrada } \mathbf x_1 \in \mathscr C_1.\\ \mathbf w^T \mathbf x_2 &\leq 0\text{ para cada vector de entrada } \mathbf x_2 \in \mathscr C_2. \end{split} \]
Definición 6.4 (Combinador lineal) Dados \(\mathbf x = (x_1, x_2,..., x_m,1)^T\) y \(\mathbf w = (w_1,w_2,...,w_m,b)^T\), se define la función \(\mathcal V: \mathbb R^{m+1}\times\mathbb R^{m+1} \rightarrow \mathbb R\) como \(\mathcal V(\mathbf x, \mathbf w) = \mathbf w^T\mathbf x\), donde \(\mathcal V(\mathbf x, \mathbf w) = 0\) representa el hiperplano de separación entre dos regiones de decisión.
Definición 6.5 (Función limitadora) Sea \(\mathscr A\) el conjunto de todas las combinaciones lineales \(\mathcal V(\mathbf x, \mathbf w)\). Considerando \(t \in \mathscr A\), se define la función limitadora \(g\) como sigue: \[ \begin{split} g: \mathscr A &\rightarrow \{1,-1\}\\ t &\rightarrow g(t)= \begin{cases} 1 & \text{si }\quad t> 0,\\ \\-1 & \text{si }\quad t\leq 0.\end{cases} \end{split} \]
Definición 6.6 (Función perceptrón) Dadas \(\mathcal V(\mathbf x, \mathbf w)\) y \(g(t)\), se define la aplicación clasificadora \(\mathscr P: \mathbb R^{m+1}\times \mathbb R^{m+1} \rightarrow \{1,-1\}\) como \(\mathscr P(\mathbf x, \mathbf w)=g(\mathcal V(\mathbf x, \mathbf w))=\hat{y}\), donde \(\hat{y}\in \{-1,1\}\) es la salida de la función perceptrón. Además, la aplicación perceptrón posee una representación gráfica mediante un dígrafo simple, como se muestra en la Figura 6.5.
A través de la función establecida en la Definición 6.6, se desarrolla un modelo de aprendizaje supervisado de clasificación binaria denominado Perceptrón. Este modelo involucra las funciones previamente definidas con el objetivo de clasificar correctamente un conjunto de entradas \(\mathbf X\), linealmente separables en dos clases. Se aplica una regla de aprendizaje adaptativa sobre cada uno de los pesos sinápticos \((\mathbf w)\) en una cantidad finita de pasos \((n)\), proceso conocido como algoritmo de aprendizaje del Perceptrón.
Definición 6.7 (Combinador lineal del perceptrón) Considerando las entradas y los pesos sinápticos en el perceptrón, \(\mathbf x(n) = (x_1(n), x_2(n),...,x_m(n),1)^T\) y \(\mathbf w(n) = (w_1(n),w_2(n),...,w_m(n),b)^T\), se define el combinador lineal del perceptrón como
\[ \mathcal V=\mathbf w^T(n)\mathbf x(n), \]
donde \(n\) denota el número de iteraciones en la aplicación del algoritmo.
Se considera \(\mathscr H \subset \mathbf X\) como el subsepacio vectorial de entrenamiento. \(\mathscr H_1\) es el subespacio de vectores de entrenamiento \(\mathbf x_1(1),\mathbf x_1(2),...\) que pertenecen a la clase \(\mathscr C_1\), y \(\mathscr H_2\) es el espacio de vectores de entrenamiento \(\mathbf x_2(1),\mathbf x_2(2),...\) que pertenecen a la clase \(\mathscr C_2\). Se define \(\mathscr H= \mathscr H_1\cup \mathscr H_2\). Con el fin de evitar un sobreentrenamiento en alguna de las dos clases, se garantiza que \(\mathscr H_1\) y \(\mathscr H_2\) tengan la misma cardinalidad.
Dado que el perceptrón es un modelo de aprendizaje supervisado, se establece \(y(k) \in \{-1,1\}\) como la clase a la que realmente pertenece cada entrada \(x(k)\) de \(\mathscr H\). Se observa que el valor \(y(k) - \hat{y}(k)\) representa el error cometido por el Perceptrón en su clasificación, y de este error se deriva la siguiente definición:
Definición 6.8 (Función actualización por corrección del error) Se define la regla de actualización de los pesos sinápticos como sigue:
\[ \mathbf w(n+1)=\mathbf w(n)+\eta(n)[y(n)-\hat y(n)]x(n). \]
De esta manera,
\[ \mathbf{w}(n+1) = \left\{\begin{array}{lcc} \mathbf w(n)+2\eta(n) x(n)& si & y(n)=1 \text{ y }\hat{y}=-1,\\ \\\mathbf w(n) & si & y(n)=\hat{y}(n),\\ \\ \mathbf w(n)-2\eta(n)x(n) & si & y(n)=-1 \text{ y }\hat{y}=1, \end{array}\right. \]
donde \(\eta(n)=\eta>0\) es una regla de adaptación de incremento fijo llamada tasa de aprendizaje.
6.3.1 Teorema de convergencia del perceptrón
Teorema 6.1 Sean \(\mathscr H_1\) y \(\mathscr H_2\), subconjuntos de vectores de entrenamiento linealmente separables. Considere las \(m\) entradas presentadas al perceptrón, como elementos de estos dos subconjuntos. El perceptrón converge después de \(n_0\) iteraciones, en el sentido que:
\[ \mathit w(n_0)=\mathit w(n_0+1)=\mathit w(n_0+2)=\cdots, \] es un vector solución para \(n_0\leq n_{\max}\).
Prueba. Vea Sosa Jerez, Zamora Alvarado, et al. (s. f.).
6.4 Funciones de activación
La asignación entre las entradas y una capa oculta en una Red Neuronal Artificial (RNA) y una Red Neuronal Profunda (RNP) es determinada por funciones de activación. Dichas funciones propagan la información generada mediante la combinación lineal de los pesos y las entradas hacia la siguiente capa, incluyendo la capa de salida. Como se ha mencionado anteriormente, existe una analogía entre las neuronas biológicas y las redes neuronales artificiales; en este contexto, las funciones de activación son análogas a la tasa del potencial de acción disparado en el cerebro.
Las funciones de activación son transformaciones de funciones escalares a escalares que proporcionan una salida específica para cada neurona. Estas funciones introducen no linealidades en las capacidades de modelado de la red. La función de activación de una neurona (nodo) define la forma funcional de su activación. Por ejemplo, si se define una función de activación lineal como \(g(z) = z\), el valor de la neurona sería la entrada cruda \(x\) multiplicada por el peso aprendido, representando así un modelo lineal. A continuación, se describen las funciones de activación más populares.
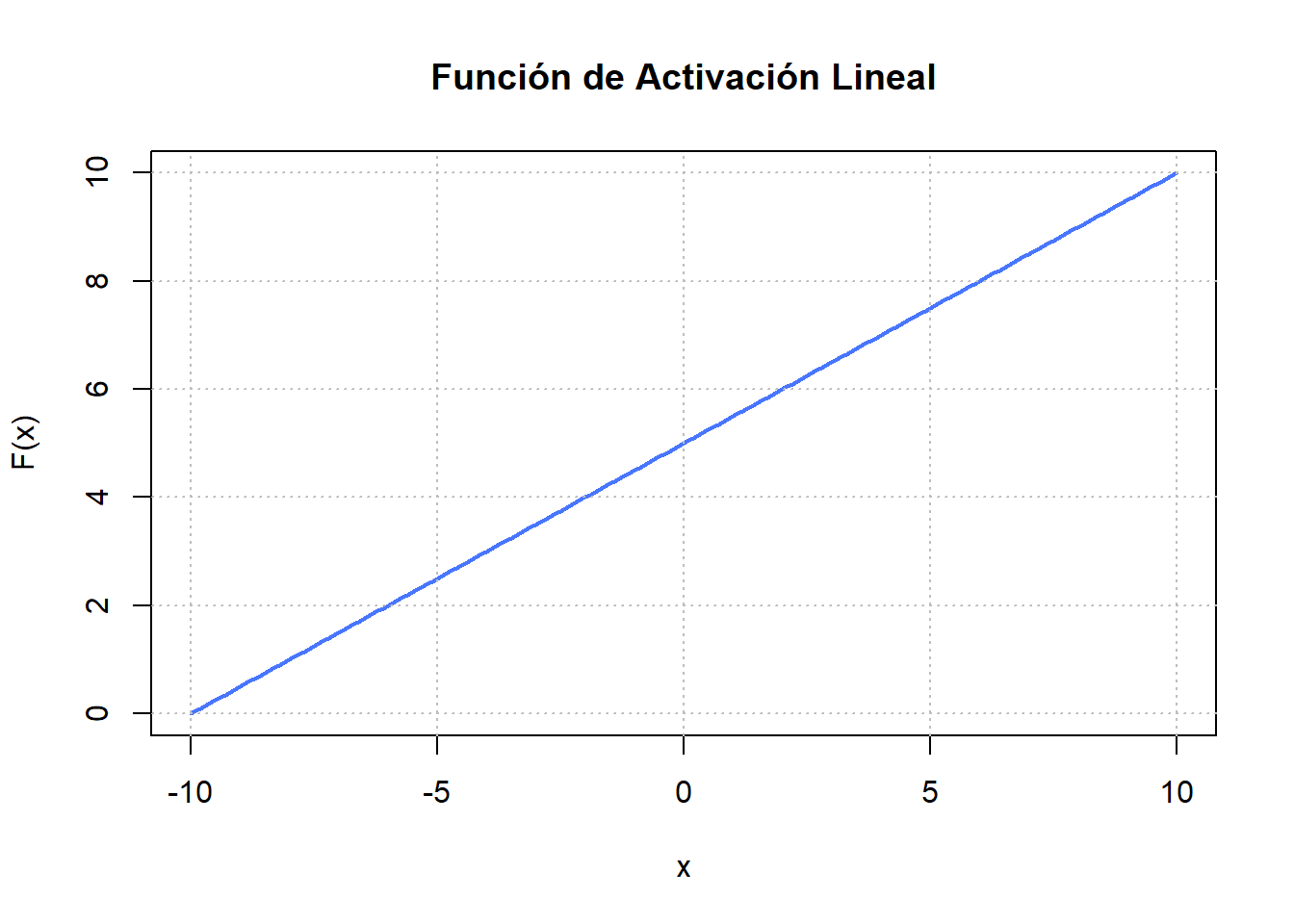
6.4.1 Lineal
La Figura 6.8 (a) exhibe una función de activación lineal que es esencialmente la función identidad. Esta se define como
\[ F(x)=Wx + b, \]
donde la variable dependiente mantiene una relación directa y proporcional con la variable independiente. En términos prácticos, esto implica que la función transmite la señal sin cambios. Sin embargo, el inconveniente al utilizar funciones de activación lineales radica en que esto no permite aprender formas funcionales no lineales.
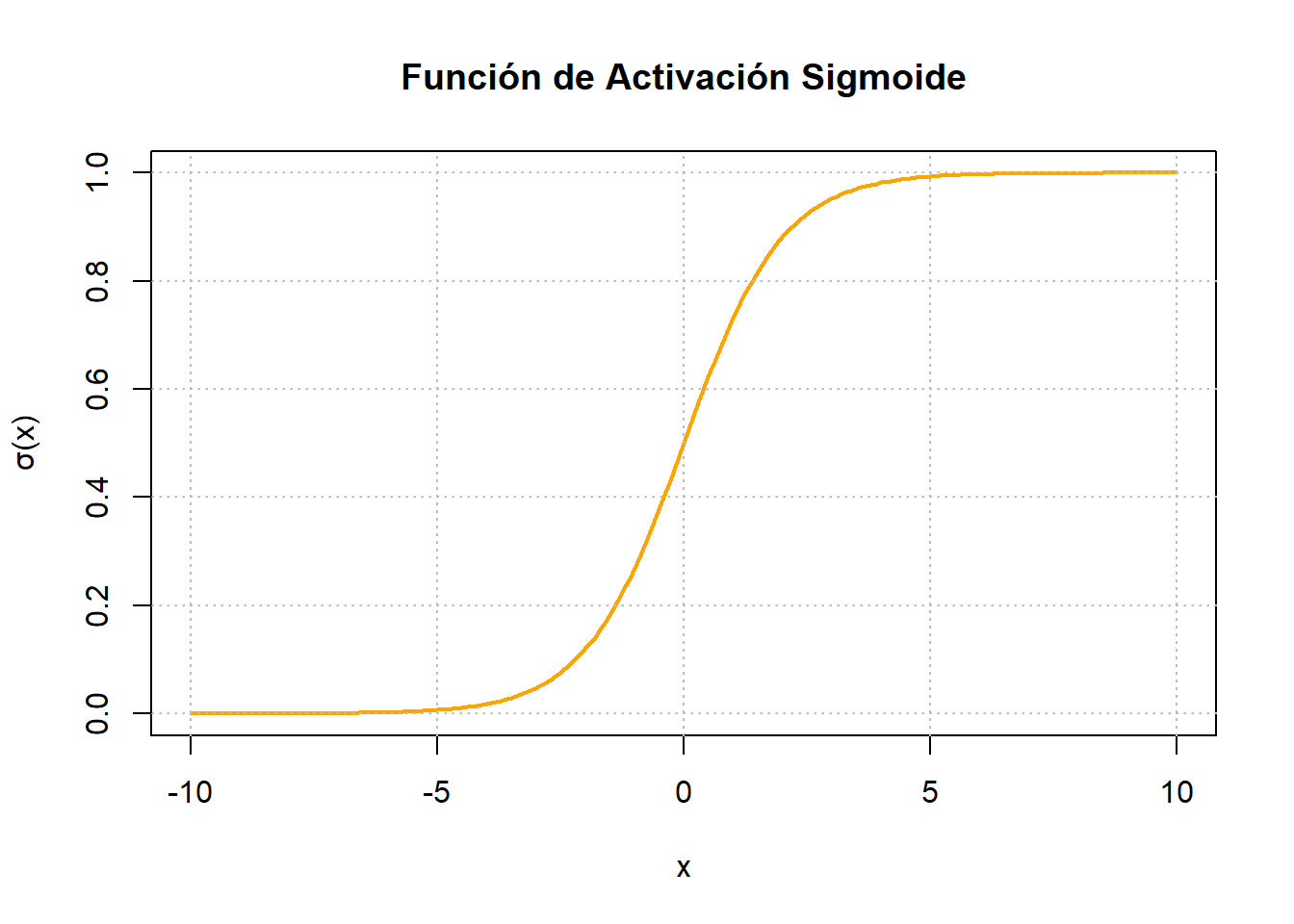
6.4.2 Sigmoide
La función de activación sigmoide desempeña el papel de un mecanismo que transforma variables independientes, abarcando un rango prácticamente infinito, en probabilidades situadas dentro del intervalo de \(0\) a \(1\). La mayor concentración de su producción tiende a agruparse estrechamente alrededor de los valores \(0\) o \(1\). Funcionando como una transformación logística, los sigmoides exhiben la capacidad de mitigar valores extremos o atípicos en los datos sin eliminarlos. Las ecuaciones que describen la función sigmoidal y su derivada son las siguientes:
\[\sigma(x) = \frac{1}{1+e^{-x}}, \quad \sigma'(x) = \frac{e^{-x}}{(1+e^{-x})^2}.\]
Ampliamente utilizada en la construcción de Redes Neuronales Artificiales (RNA) y Redes Neuronales Profundas (DNN), especialmente en escenarios donde el resultado deseado es una probabilidad o un resultado binario, la función de activación sigmoide representa uno de los tipos más frecuentemente empleados.
La función de activación \(\sigma(x):\mathbb R\to [0,1]\) se caracteriza por ser una función suave y diferenciable en todo punto. Compacta cualquier valor entre \(0\) y \(1\) y destaca por su naturaleza estrictamente creciente, logrando un delicado equilibrio entre comportamiento lineal y no lineal. Sin embargo, es susceptible de experimentar “atascos”, un fenómeno en el cual los valores de salida convergen muy cerca de \(1\) o \(0\), especialmente cuando los valores de entrada son muy positivos o negativos (consulte la Figura 6.8 (b)). Al referirnos a que la función de activación se “atasca”, implicamos que el proceso de aprendizaje deja de mejorar debido al dominio de valores de salida grandes o pequeños dentro de esta función de activación.
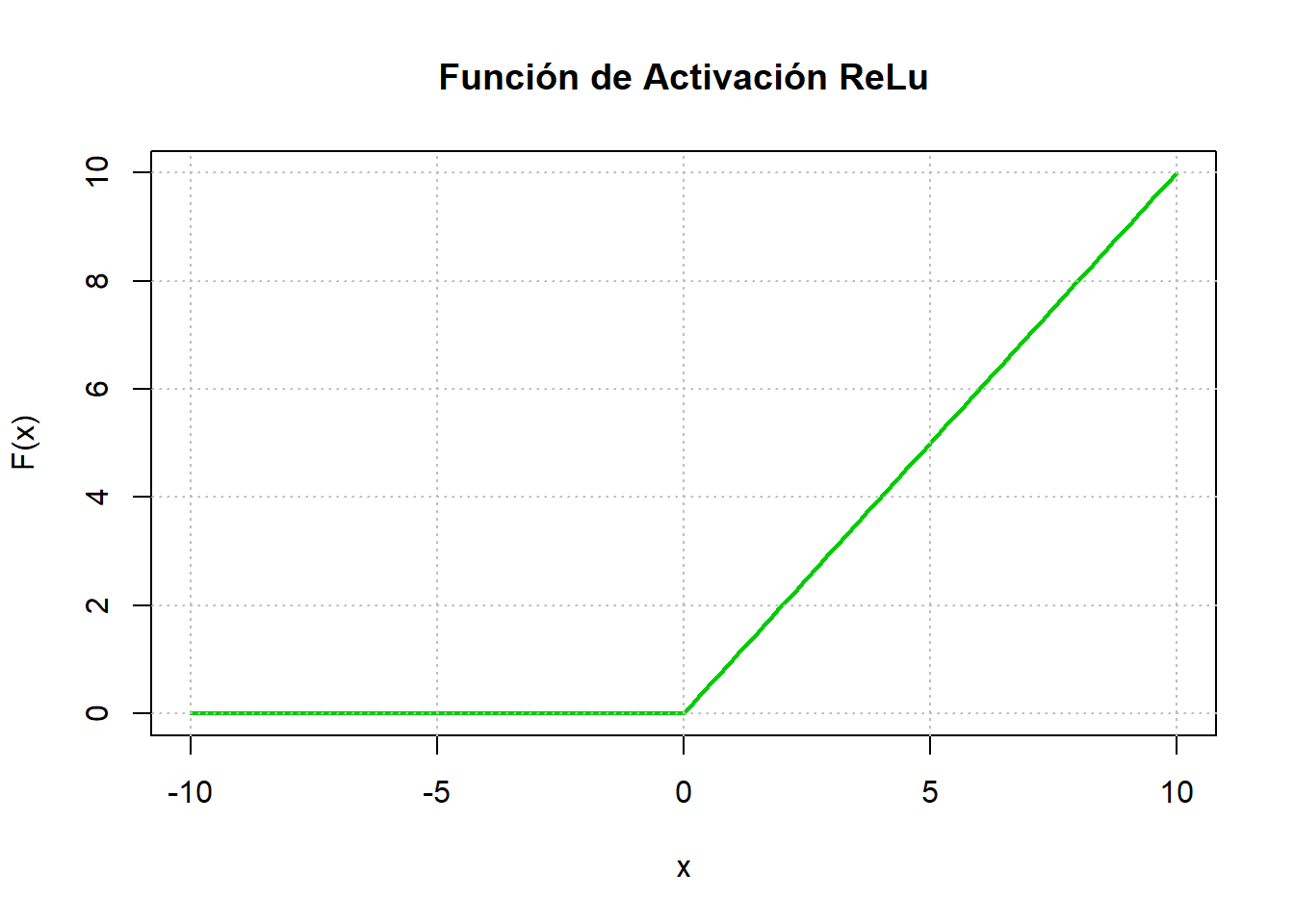
6.4.3 Unidad lineal rectificadora (ReLu)
La función de activación de la unidad lineal rectificadora (ReLU) destaca como una de las más adoptadas. Exhibe una respuesta plana por debajo de un umbral especificado, normalmente establecido en cero, y luego se vuelve lineal. La activación en una ReLU se produce solo cuando la entrada supera un determinado umbral. Cuando la entrada está por debajo de cero, la salida sigue siendo cero, pero al exceder el umbral, como se ilustra en la Figura 6.8 (c), establece una relación lineal con la variable dependiente, de la siguiente manera
\[ F(x)=\max(0,x). \]
A pesar de su aparente simplicidad, la función de activación de ReLU facilita las transformaciones no lineales, lo que permite la aproximación de funciones no lineales arbitrarias mediante el uso de rectificadores lineales suficientes. Esto contrasta con los escenarios en los que se emplean exclusivamente funciones de activación lineal.
En la actualidad, las ReLU representan el estado de la técnica, demostrando su eficacia en diversas situaciones. Sin embargo, debido a que el gradiente de la ReLU es cero o una constante, plantea desafíos en el control de problemas como la desaparición y la explosión de gradientes, comúnmente conocido como el problema de la “ReLU moribunda”. En particular, las funciones de activación de ReLU han mostrado un rendimiento de entrenamiento superior en la práctica en comparación con las funciones de activación sigmoide. Esta función de activación se emplea más comúnmente en capas ocultas y capas de salida cuando la variable de respuesta es continua y supera cero.
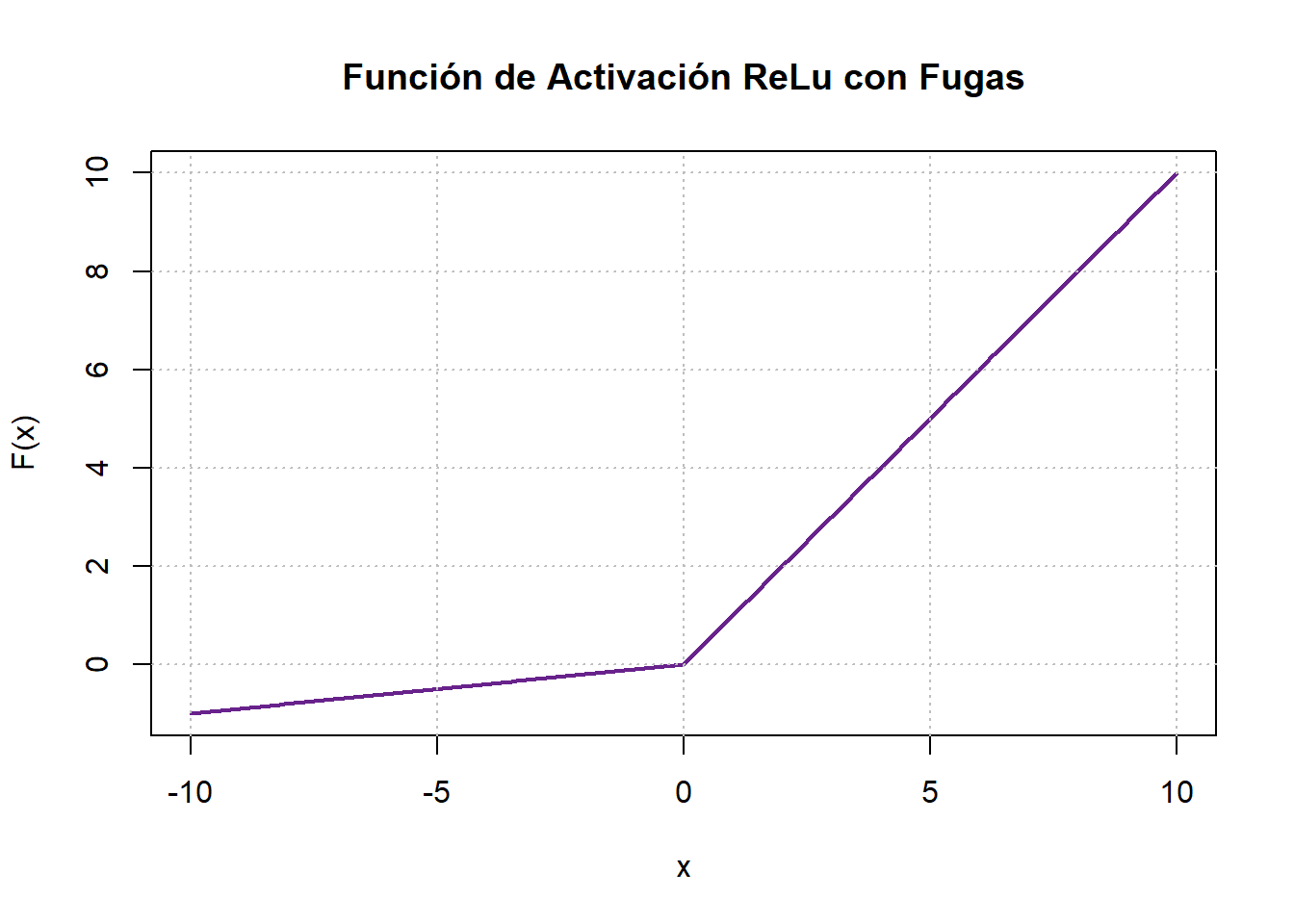
6.4.4 ReLu con fugas
Las ReLU con fugas sirven como medida correctiva para abordar el fenómeno de la “ReLU moribunda”. A diferencia de la ReLU convencional, que asigna un valor cero a la función cuando \(x < 0\), la ReLU con fugas introduce una pequeña pendiente negativa, denotada como \(\alpha\), donde \(\alpha\) es un valor escalar dentro del rango de \(0\) a \(1\) (consulte la Figura 6.8 (d)). Si bien esta variación de ReLU ha demostrado cierto éxito en aplicaciones prácticas, los resultados no son uniformemente consistentes. La expresión matemática de esta función de activación se proporciona a continuación:
\[ F(x)=\begin{cases}x & \text{si}\quad x>0,\\ \alpha x& \text{otro caso.}\end{cases} \]
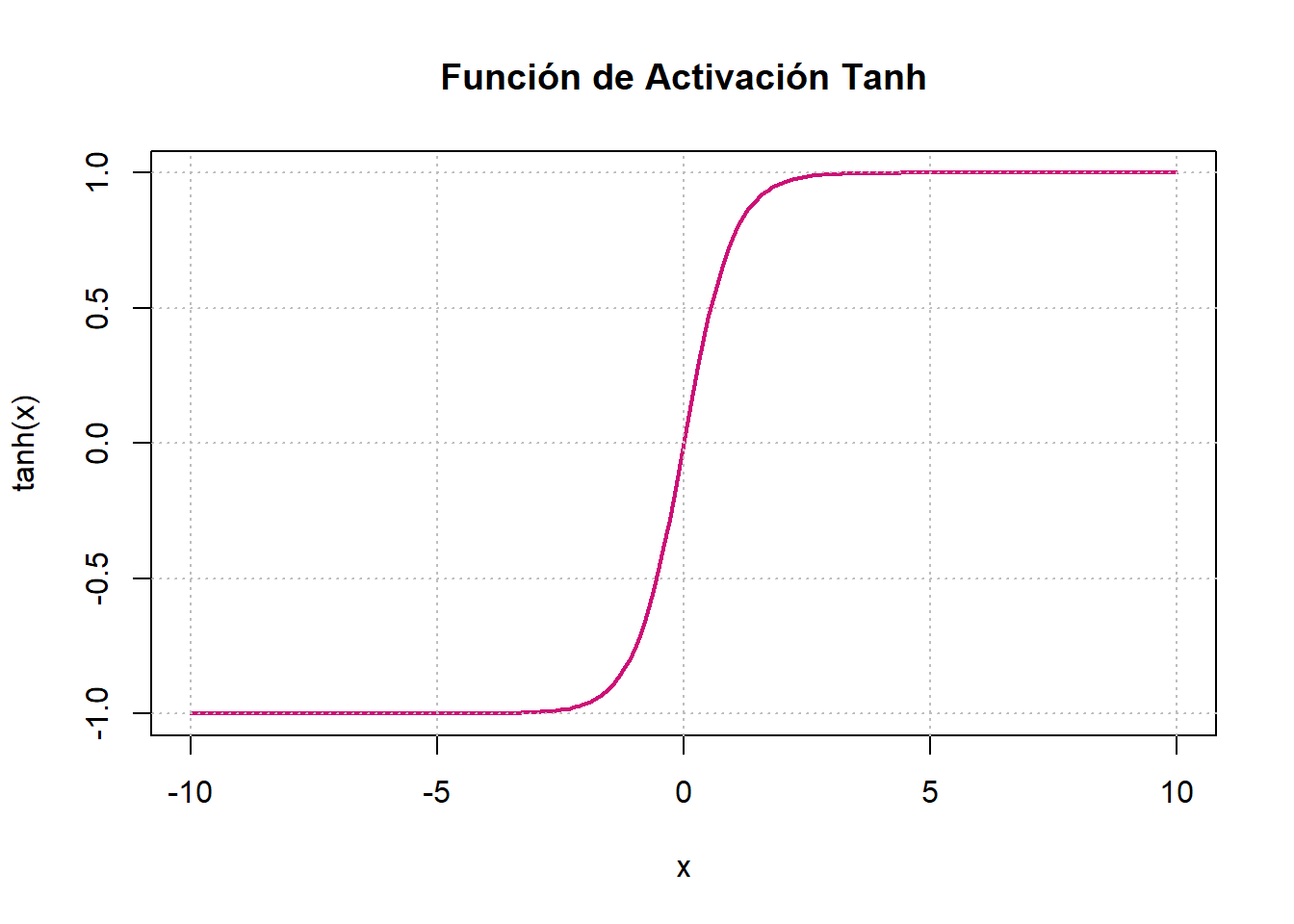
6.4.5 Tangente hiperbólica
La función de activación tangente hiperbólica \((\tanh)\) es una modificación de la función sigmoide y se define como
\[ \tanh(x)=\frac{e^x-e^{-x}}{e^{x}+e^{-x}}. \]
Cuyas gráficas se observan en la Figura 6.8 (e). La función de activación tangete hiperbólica \(\tanh(x):\mathbb R\to [-1,1]\) es una función suave y diferenciable en todo punto. Similar a la función de activación sigmoide, produce una salida sigmoidal (en forma de “S”). Sin embargo, la función \(\tanh\) tiene la ventaja de ser menos propensa al problema de “atascarse” en comparación con la función de activación sigmoide. Esto se atribuye a que los valores de salida de la función \(\tanh\) se encuentran dentro del rango de \(-1\) a \(1\). En consecuencia, a menudo se prefiere la función de activación \(\tanh\) para capas ocultas. Una ventaja adicional de \(\tanh\) es su capacidad para manejar los números negativos de manera más efectiva. Sin embargo, el gradiente de la función evaluado en valores muy alejados al origen será un valor muy pequeño, por lo que sigue generando un estancamiento en el proceso de retropropagación.
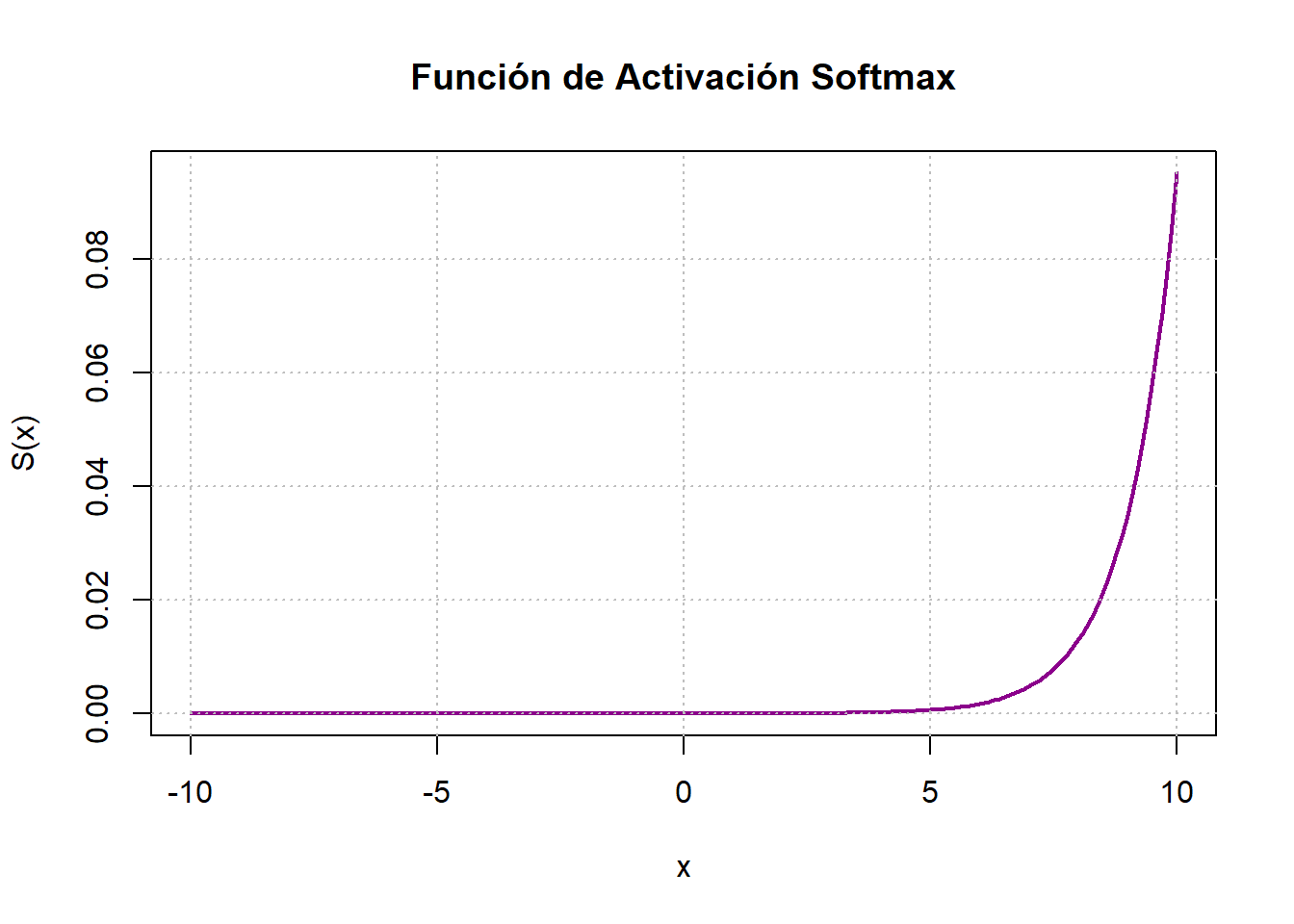
6.4.6 Softmax
La función Softmax se emplea predominantemente en redes neuronales dedicadas a abordar problemas de clasificación. Su resultado proporciona un porcentaje que indica la probabilidad de que los datos ingresados pertenezcan a cada una de las clases. Es habitual utilizar esta función de activación en las capas finales de la red neuronal. La expresión que la define es:
\[ S=\frac{e^{a_i^l}}{\sum_{k=1}^K (e^{a_k^l})}, \text{ para }i=1,\ldots, K \]
donde \(a\) es la salida de las capas ocultas y \(K\) es el número de clases en el modelo. La Figura 6.8 (f) ejemplifica esta función de activación.
6.5 Funciones de coste
Las funciones de costo, pérdida u objetivo desempeñan un papel fundamental al medir la disparidad entre los resultados obtenidos y los valores deseados. En el contexto del descenso del gradiente, estas funciones son cruciales, ya que buscan minimizar la salida de la función de costo, lo que lleva a que los valores generados por la red neuronal sean cercanos a los valores deseados.
Para ser empleada en el proceso de retropropagación, la función de costo debe cumplir con dos propiedades fundamentales:
- La función de costo \(C\) debe expresarse como un promedio:
\[C = \frac{1}{n} \sum_{x} \mathcal L_x, \]
donde \(\mathcal L_x\) representa las funciones de pérdida para ejemplos individuales \(x\) en el conjunto de entrenamiento.
- La función de costo \(C\) no debe depender de ningún valor de activación, excepto los valores de salida \({a}^L\). Si la función de costo depende de otras capas de activación además de la capa de salida, la retropropagación no será válida, ya que la idea de propagación hacia atrás dejará de funcionar.
Observación. Es importante destacar que la función de costo y la función de pérdida son conceptos distintos. La función de costo representa el promedio de las pérdidas de todas las muestras o datos de entrenamiento, mientras que la función de pérdida se refiere a las pérdidas individuales para cada ejemplo. A pesar de esta diferencia, es común observar el uso de ambos términos de manera intercambiable o con propósitos similares en la literatura.
6.6 Gradiente descendente
El gradiente o vector gradiente se presenta como una generalización de la derivada en varias variables, su definición formal se muestra a continuación.
Definición 6.9 (Vector gradiente) Sea \(f : U \subseteq \mathbb{R}^n \rightarrow \mathbb{R}\) una función diferenciable definida en el conjunto abierto \(U\in \mathbb R^n\). Se define el vector gradiente de la función \(f\) en el punto \(x_0\) de \(U\), denotado por \(\nabla f(x_0)\), como el vector en \(\mathbb{R}^n\) dado por
\[\nabla f(x_0) = \left( \frac{\partial f}{\partial x_1}(x_0), \frac{\partial f}{\partial x_2}(x_0), \ldots, \frac{\partial f}{\partial x_n}(x_0) \right).\]
Adicionalmente, el vector gradiente señala la dirección en la cual la función \(f\) experimenta el crecimiento más rápido. Este resultado se formaliza mediante el siguiente teorema
Teorema 6.2 Sea \(f : X \subseteq \mathbb{R}^n \rightarrow \mathbb{R}\) diferenciable en \(x_0 \in X\), el gradiente apunta hacia la dirección de mayor crecimiento de \(f\).
Prueba. Vea Stewart (2017).
El método de descenso del gradiente desempeña un papel fundamental en el entrenamiento de las redes neuronales. A través de este método, se logra considerar los valores más óptimos y eficaces, específicamente los pesos \(w\) de la red neuronal. Este enfoque permite estimar cada nuevo parámetro basándose en el anterior, teniendo en cuenta la derivada de la función de coste. Además, el proceso presenta ventajas como la simplicidad y la rapidez de convergencia.
6.6.1 Algoritmo gradiente descendente
Considere una función de costo \(\mathcal C\) definida como \(\mathcal C : \Omega \subseteq \mathbb{R}^n \rightarrow \mathbb{R}\). El algoritmo de gradiente descendente es utilizado para encontrar un valor \(w\) en \(\Omega\) tal que \(\mathcal C(w)\) alcance un mínimo (extremo local).
Las actualizaciones de \(w\) se realizan de la siguiente manera:
\[w_{k+1} = w_k - \alpha \nabla\mathcal C(w_k),\]
donde \(\alpha\) es la tasa de aprendizaje y \(k\) es el número de iteraciones. Se elige inicialmente un valor inicial \(w_0\) (puede ser seleccionado de forma aleatoria o elegido manualmente). El algoritmo comienza en este punto con el propósito de ajustar el valor del peso inicial hasta situarlo en el mínimo de la función.
6.7 Perceptrón Multicapa
Como se expuso previamente en la Sección 6.2.2, se pueden representar mediante un diagrama simple, que incluye nodos ponderados y un conjunto de atributos que las caracterizan. En esta sección, la estructura de la red será formalizada junto con sus definiciones correspondientes (Sosa Jerez, Zamora Alvarado, et al. (s. f.)).
Definición 6.10 (Perceptrón Multicapa (MLP)) Una red neuronal artificial MLP se define formalmente como una tripla \(\langle\mathscr D, \{f\}, \mathscr A\rangle\), donde;
\(\mathscr D\) es un dígrafo contable, localmente finito, con nodos etiquetados. Sus vértices corresponden a los nodos de procesamiento (neuronas), mientras que las etiquetas de los nodos, denominadas pesos, representan las intensidades de las conexiones sinápticas. Dichas intensidades se denotan por \(w_{ij}\), indicando el peso de la conexión entre la neurona \(j\)-ésima y la \(i\)-ésima.
\(\mathscr A\) es el conjunto que contiene los elementos de “entrada” de las unidades o nodos de procesamiento, generalmente representado por \(A =\mathbb R\).
\(\{f: \mathscr A\to\mathscr A\},\) es una colección de funciones de activación.
En el dígrafo \(\mathscr D\), se definen las capas como las columnas de vértices en \(\mathscr D\). Cada una de estas columnas puede ser representada matemáticamente a través de un vector, de la siguiente manera:
Capa de entrada: corresponde a la primera columna de vértices de \(\mathscr D\), cuya representación matemática se expresa como: \[\mathbf x = (x_1, \ldots, x_{d_0})^T \text{ donde } \mathbf x \in \mathbb{R}^{(d_0 \times 1)}.\]
Capa de salida: corresponde a la última columna de vértices de \(\mathscr D\), cuya representación matemática se describe como: \[\hat{\mathbf y} = (\hat{y}_1, \ldots, \hat{y}_{d_L})^T \text{ donde } \hat{y}\in\mathbb{R}^{(d_L\times 1)}.\]
Capas ocultas: corresponden a las columnas intermedias entre la capa de entrada y la de salida. Su representación matemática está dada por: \[\begin{split} \mathbf a^l &= (a_{1}^l, \ldots, a_{d_l}^l)^T \text{ donde } a^l\in\mathbb{R}^{(d_l\times 1)}\\ &= f^l(z^l)\text{ con } l = 1, \ldots, L - 1. \end{split}\]
Cabe destacar que cada \(\mathbf a^l\) corresponde a una columna de vértices en \(\mathscr D\), donde \(L\) denotará la totalidad de capas en la red. \(f^l\) será una función de activación vectorial y \(z^l\) será el combinador lineal matricial, ambos en la capa \(l\). De esta manera, la capa de salida también puede representarse como el vector \(\mathbf a^L\), y la capa de entrada como el vector \(\mathbf a^0\).
Definición 6.11 (Neuronas o nodos de procesamiento) Las neuronas de la red MLP son los vértices de las capas ocultas en \(\mathscr D\), es decir, las componentes de \(\mathbf a^l\) se denotarán como \(a_i^l\), donde:
\[ a_i^l=f^l(z_i^l). \]
Definición 6.12 (Función de activación) Se define \(f^l\) como una función de activación vectorial, de modo que:
\[ f^l: \mathbb R^{(d_1\times 1)}\rightarrow \mathbb R^{(d_1\times 1)}. \]
Definición 6.13 (Matriz de pesos) Para cada capa \(l\) en \(\mathscr D\), se define \(\mathbf w^l\) como una matriz de dimensiones \(d_l \times d_{l-1}\), donde \(d_l\) representa la cantidad de neuronas en la capa \(l\), de la siguiente manera:
\[ \mathbf w^l=\begin{bmatrix}w_{11}^l & \cdots & w_{1j}^l&\cdots&w_{1d_{l-1}}^l\\ \vdots &\cdots&\vdots&\cdots&\vdots\\ w_{i1}^l & \cdots & w_{ij}^l&\cdots&w_{id_{l-1}}^l\\ \vdots &\cdots&\vdots&\cdots&\vdots\\ w_{d_l1}^l & \cdots & w_{d_lj}^l&\cdots&w_{d_ld_{l-1}}^l \end{bmatrix} \]
Definición 6.14 (Sesgo) Se define el sesgo como el vector
\[ \mathbf b^l=(b_1^l,\ldots,b_{d_l}^l)^T\quad\text{con }\mathbf b^l\in\mathbb R^{(d_1\times 1)} \]
correspondiente a la capa \(l\), cuyas entradas son el parámetro de sesgo de cada neurona.
Definición 6.15 (Combinador lineal matricial) Dados \(\mathbf a^{l-1}, \mathbf w^l\) y \(\mathbf b^l\) se define el combinador lineal como
\[ \begin{split} \mathbf z^l&=(z_1^l,\ldots,z_{d_l}^l)^T\\ &=\mathbf w\mathbf a^{l-1}+\mathbf b^l, \end{split} \]
donde
\[ z_i^l=\sum_{j=1}^{d_{l-1}}w_{ij}^la_j^{l-1}+b_i. \tag{6.2}\]
Se observa que la ecuación (6.2) guarda una fuerte relación con la Definición 6.4. No obstante, en el caso de \(\mathbf{z}^l\), se ha incorporado el vector de parámetros de sesgo \(\mathbf{b}^l\).
Definición 6.16 (Función de pérdida) Se define \(\mathcal L: \mathbb{R}^n \rightarrow \mathbb{R}\) de manera que
\[\begin{split}\mathcal L(\mathbf y,\mathbf{\hat{y}}) &= \frac{1}{2}\|\mathbf y - \mathbf{\hat{y}}\|^2\\ &= \frac{1}{2} \|\mathbf y - \mathbf a^L\|^2\\ &= \frac{1}{2} \sum_{r=1}^{d_L} (y_r - a_r^L)^2,\end{split}\] como la función de pérdida de la red MLP.
Definición 6.17 (Conjunto de datos de entrenamiento) Sea \(\mathbf X = (\mathbf x(1), \ldots, \mathbf x(n))\), donde \(\mathbf x(k)\), con \(k = 1, \ldots, n\), representa el \(k\)-ésimo dato en el conjunto \(\mathbf X\), siendo este el vector de entradas de la red neuronal en la \(k\)-ésima etapa.
Definición 6.18 (Conjunto de salidas de la red) Se define \(\hat{\mathbf Y} = (\hat{\mathbf y}(1), \ldots, \hat{\mathbf y}(n))\), donde \(\hat{\mathbf y}(k)\), con \(k = 1, \ldots, n\), representa el \(k\)-ésimo dato en el conjunto \(\hat{\mathbf Y}\), siendo este el vector de salidas de la red neuronal en la \(k\)-ésima etapa.
Definición 6.19 (Resultados esperados) Se define \(\mathbf Y = (\mathbf y(1), \ldots, \mathbf y(n))\), donde \(\mathbf y(k)\), con \(k = 1, \ldots, n\), representa el \(k\)-ésimo dato en el conjunto \(\mathbf Y\), siendo este el vector de resultados esperados correspondiente al dato \(\mathbf x(k)\).
6.7.1 Entrenamiento y aprendizaje del Perceptrón Multicapa
El proceso de aprendizaje de una red neuronal se configura como un modelo de aprendizaje supervisado. En este proceso, se establece un algoritmo que, a partir de un conjunto de datos de entrenamiento que incluye entradas y resultados esperados, permite el entrenamiento gradual de la red. El objetivo principal es que la red pueda calcular de manera autónoma los valores óptimos de pesos y sesgos para clasificar las entradas en salidas, minimizando la discrepancia con respecto a los resultados esperados.
Al concluir este proceso de entrenamiento, se espera que la red neuronal desarrolle la capacidad de clasificar cualquier dato, incluso aquellos no presentes en el conjunto de entrenamiento inicial (datos de prueba), generando salidas con un error de clasificación mínimo. Este proceso de entrenamiento se compone de dos etapas esenciales: la propagación hacia adelante o feedforward, y la retropropagación, también conocida como back-propagation.
6.7.1.1 Propagación hacia adelante
El proceso de prealimentación constituye la base del entrenamiento y aprendizaje de la red, considerando los siguientes pasos:
Se elige un vector de datos \(\mathbf x \in \mathbf X\) como entrada de la red neuronal MLP.
Se establecen matrices \(\mathbf w^l\) de pesos y vectores \(\mathbf b^l\) de sesgo, cuyas componentes tienen entradas aleatorias que pertenecen a un umbral prefijado.
Se “alimenta” la red neuronal en una única dirección. Para ello, se inicia estableciendo lo que se tendrá en la primera capa de procesamiento y luego se generaliza el proceso:
Alimentación primera capa: Se establecen los productos matriciales en cada nodo de procesamiento, dados por:
\[ \begin{split}\mathbf z^1&=(\mathbf w^1\mathbf x)+\mathbf b^1\\ \mathbf a^1&=f^1(\mathbf z^1).\end{split} \]
Generalización: Considerando cómo se “alimenta” la red en la primera capa, se repite el mismo proceso para cada capa siguiente:
\[ \begin{split}\mathbf z^l&=(\mathbf w^l\mathbf a^{l-1})+\mathbf b^l\\\mathbf a^l&= f^l(\mathbf z^l).\end{split} \]
Se observa que en este paso, lo que en la primera capa era \(\mathbf x\), en cualquier capa diferente será \(a^{l-1}\). Esto se debe a que la red es un dígrafo \(\mathscr D\), donde la salida de la capa anterior \((l - 1)\) se convierte en el vector de entrada para la capa siguiente \((l)\).
6.7.1.2 Retropropagación
La retropropagación se emplea en las redes neuronales como algoritmo de aprendizaje, y su objetivo es ajustar de manera eficiente los pesos de la red. Este proceso consiste en establecer inicialmente de manera aleatoria los pesos requeridos en la red para obtener una salida, la cual se compara mediante la función de pérdida \(\mathcal L\) con el resultado esperado. De esta manera, se calcula el error de aproximación de la red con el objetivo de minimizar dicho error a través de la optimización de la función \(\mathcal L\). La optimización se realiza mediante una generalización del algoritmo de descenso del gradiente, utilizando la regla de la cadena y recorriendo la red de atrás hacia adelante.
De forma iterativa, la red aprende a establecer los pesos y sesgos adecuados para cada neurona, con el fin de obtener una salida que se aproxime al resultado esperado. Para comprender el funcionamiento del algoritmo de retropropagación, es necesario comenzar calculando las derivadas respecto a los parámetros de pesos y sesgos de la función de coste en la red prealimentada.
Se inicia calculando la derivada de \(\mathcal L\) respecto a uno de los pesos que afectan a la última capa:
\[\begin{split}\frac{\partial \mathcal L}{\partial w_{ij}^L} &= \frac{1}{2} \sum_{r=1}^{d_L} \frac{\partial}{\partial w_{ij}^L} (y_r - a_{r}^L)^2\\ &= \sum_{r=1}^{d_L} (a_{r}^L - y_r) \left(\frac{\partial a_r^L}{\delta w_{ij}^L}\right)\\ &=\sum_{r=1}^{d_L} (a_{r}^L - y_r) \frac{\partial}{\partial w_{ij}^L}f^L(z_{r}^L)\\ &= \sum_{r=1}^{d_L} (a_{r}^L - y_r) \frac{\partial}{\partial w_{ij}^L}f^L\left(\sum_{t=1}^{d_L}w_{rt}^La_t^{L-1}+b_r^L\right).\end{split} \tag{6.3}\]
Esta expresión se anula en todos los valores en los que \(r\neq i\) o \(t\neq j\). Si \(r = i\) y \(t = j\), se tiene:
\[\frac{\partial \mathcal L}{\partial w_{ij}^L} = (a_{i}^L - y_i) f^{(1)L}(z_{i}^L) a_j^{L-1}. \tag{6.4}\]
La ecuación (6.4) proporciona la derivada particular de la función de pérdida respecto a un único peso. Para generalizar esta situación y calcular \(\frac{\partial \mathcal L}{\partial \mathbf w^{L}}\), se deben tener en cuenta las dimensiones y definir una nueva operación matricial.
Definición 6.20 (Producto Hadamard) Dadas \(A, B\) dos matrices de dimensión \((m\times n)\), el producto de Hadamard \((A\odot B)\) es una matriz de dimensión \((m\times n)\) tal que:
\[ (A\odot B)_{ij}=[a_{ij}b_{ij}]. \]
Generalizando la ecuación (6.4) y haciendo uso de la definición previa, se puede expresar la derivada parcial de la función de pérdida respecto a los pesos en la última capa como:
\[\begin{split}\frac{\partial \mathcal L}{\partial \mathbf w^L} &= \frac{\partial \mathcal L}{\partial \mathbf a^L}\frac{\partial \mathbf a^L}{\partial \mathbf z^L}\frac{\partial \mathbf z^L}{\partial \mathbf w^L}\\&= \left[(\mathbf a^L - y)\odot f^{(1)L}(\mathbf z^L)\right] (\mathbf a^{L-1})^T,\end{split} \tag{6.5}\]
donde el error en la última capa se denota como \((\mathbf a^L - y)\) y se representa como \(\mathbf e^L\). También se introduce la notación \(\delta^L\) para referirse al producto de Hadamard \([(\mathbf a^L - y)\odot f^{(1)L}(\mathbf z^L)]\). La expresión se simplifica como:
\[\frac{\partial \mathcal L}{\partial \mathbf w^L} = \delta^L (a^{L-1})^T. \tag{6.6}\]
Al extender este proceso de las ecuaciones (6.3) a (6.6) para calcular \(\frac{\partial \mathcal L}{\partial \mathbf b^L}\), se obtiene:
\[\frac{\partial \mathcal L}{\partial \mathbf b^L} = \delta. \tag{6.7}\]
Se reconoce que la función de pérdida \(\mathcal L\) en el conjunto de datos \(\mathscr D\) depende de las matrices de pesos y los vectores de sesgo de cada capa. Por lo tanto, se busca minimizar la función de pérdida en cada capa \(l\). Al considerar las derivadas en la capa \(L-1\), se obtiene:
\[ \begin{split}\frac{\partial \mathcal L}{\partial \mathbf w^{L-1}}&= \frac{\partial \mathcal L}{\partial \mathbf a^{L}}\frac{\partial \mathbf a^L}{\partial \mathbf z^{L}}\frac{\partial \mathbf z^L}{\partial \mathbf a^{L-1}}\frac{\partial \mathbf a^{L-1}}{\partial \mathbf z^{L-1}}\frac{\partial \mathbf z^{L-1}}{\partial \mathbf w^{L-1}}\\ &= [((\mathbf w^L)^T \delta^L)\odot f^{L-1(1)}(\mathbf z^{L-1})](\mathbf a^{L-2})^T\\ &= \delta^{L-1}(\mathbf a^{L-2})^T,\end{split} \tag{6.8}\]
donde \(((\mathbf w^L)^T \delta^L) = \mathbf e^{L-1}\) y \([((\mathbf w^L)^T \delta^L)\odot f^{L-1}(\mathbf z^{L-1})] = \delta^{L-1}\).
De manera análoga, la derivada parcial de la función de pérdida con respecto al sesgo en la capa \(l-1\) se expresa como:
\[\frac{\partial \mathcal L}{\partial \mathbf b^{L-1}} = \delta^{L-1}. \tag{6.9}\]
Al generalizar este proceso, se obtiene la relación recurrente para \(\delta^l\):
\[\delta^l = \left[((\mathbf w^{l+1})^T \delta^{l+1})\odot f^l(\mathbf z^l) \right], \quad \text{para } l = L-1, \ldots, 1.\]
De esta forma, las derivadas parciales de la función de pérdida respecto a los pesos y sesgos en cada capa se expresan como:
\[\frac{\partial \mathcal L}{\partial \mathbf w^l} = \delta^l (a^{l-1})^T,\quad \frac{\partial \mathcal L}{\partial \mathbf b^l} = \delta^l. \tag{6.10}\]
Con estas expresiones, se define el proceso iterativo de retropropagación en los siguientes pasos:
Calcular el error \(\mathbf e^L\) y \(\delta^L\) en la última capa, como se muestra en las ecuaciones (6.5) y (6.6).
Calcular \(\mathbf e^l\) y \(\delta^l\) en cada capa \(l\) mediante las relaciones:
\[ \begin{cases}\mathbf e^l&= (\mathbf w^{l+1})^T\delta^{l+1}\\ \delta^l &= (f^{l(1)}(\mathbf z^l))\odot \mathbf e^l.\end{cases} \]
Proceder a la actualización de pesos y sesgos. Para ello, se introduce la función de coste \(\mathcal C\) aplicada a la pérdida \(\mathcal L\) y se calculan las derivadas con respecto a los pesos y sesgos:
\[ \mathcal C=\frac{1}{n}\sum_{k=1}^n \mathcal L(\mathbf y, \mathbf{\hat{y}})(k). \]
Estas derivadas son equivalentes a las obtenidas en las ecuaciones (6.6), (6.7) y (6.10). Luego, se aplica el algoritmo de descenso del gradiente para actualizar las matrices de pesos y sesgos:
\[ \begin{split}\frac{\partial \mathcal C}{\partial \mathbf w^l}&=\frac{1}{n}\sum_{k=1}^n \frac{\partial}{\partial \mathbf w^l}\mathcal L(\mathbf y, \hat{\mathbf y})(k)\\ &=\nabla_{\mathbf w^l}\mathcal C.\\ \frac{\partial\mathcal C}{\partial\mathbf b^l}&= \frac{1}{n}\sum_{k=1}^n \frac{\partial}{\partial \mathbf b^l}\mathcal L(\mathbf y, \hat{\mathbf y})(k)=\nabla_{\mathbf b^l}\mathcal C.\end{split} \tag{6.11}\]
Note que en la ecuación (6.11), las derivadas con respecto a \(\mathbf w^L\) y \(\mathbf b^L\), son las mismas que se dedujeron en la ecuación (6.10), con estos últimos parámetros obtenidos, se puede aplicar el algoritmo del descenso del gradiente, para actualizar las matrices de pesos y sesgos, así:
\[ \begin{cases}\mathbf w^l(t)&:= \mathbf w^{l-1}(t-1)-\eta\nabla_{\mathbf w^l}\mathcal C,\\ \mathbf b^l(t)&:= \mathbf b^{l-1}(t-1)-\eta\nabla_{\mathbf b^l}\mathcal C,\end{cases} \]
donde \(t\) representa el iterador de épocas asignadas a la red.
Al aplicar estos algoritmos (Feed-Forward y Backpropagation), se puede construir una red neuronal que, a partir de un conjunto de datos (ya sea de prueba o entrenamiento), se entrena para lograr una clasificación precisa de los datos. Es importante destacar que antes de aplicar el conjunto de prueba a la red, se debe realizar un proceso de preprocesamiento de datos, que incluye la eliminación de datos atípicos y la normalización del conjunto de entrenamiento, con el fin de evitar confusiones en la clasificación.
6.8 Evaluación de modelos de aprendizaje automático
Una vez entrenado un modelo de Machine Learning con datos etiquetados, se espera que funcione correctamente con nuevos datos. Sin embargo, es crucial asegurar la precisión de las predicciones del modelo en condiciones de producción.
Para lograr este objetivo, es imprescindible validar el modelo. Este procedimiento implica determinar si los resultados digitales que cuantifican las relaciones hipotéticas entre las variables son adecuados como descripciones de los datos.
Con el propósito de evaluar el rendimiento de un modelo de Machine Learning, es necesario ponerlo a prueba con datos nuevos. A partir del desempeño del modelo con datos desconocidos, se puede determinar si requiere ajustes adicionales, si ha sido sobreajustado o si está generalizado de manera adecuada.
Una de las técnicas más utilizadas para evaluar la eficacia de un modelo de Machine Learning es la validación cruzada. Este método, que también se considera un procedimiento de re-muestreo, permite evaluar un modelo incluso cuando se cuenta con datos limitados.
Para llevar a cabo la validación cruzada, es necesario reservar previamente una parte de los datos de entrenamiento. Estos datos no se emplearán durante el proceso de entrenamiento del modelo, sino que se utilizarán posteriormente para probarlo y validar sus resultados.
Frecuentemente en el ámbito del Machine Learning, la validación cruzada se emplea para comparar diferentes modelos y seleccionar aquel que sea más apropiado para un problema específico. Esta técnica, además de ser fácil de comprender e implementar, presenta menos sesgos que otros métodos. A continuación se exploran las principales técnicas de validación cruzada.
6.8.1 División de datos en entrenamiento y prueba
El enfoque denominado división de datos en entrenamiento y prueba se basa en la aleatoria división de una serie de datos en dos conjuntos. Uno de estos conjuntos se destina al entrenamiento del modelo de Machine Learning, mientras que el otro se reserva para la validación del mismo.
Generalmente, se asigna entre un \(70\%\) y un \(80\%\) de los datos totales para el entrenamiento, dejando el \(20-30\%\) restante para llevar a cabo la validación cruzada.
Aunque esta técnica suele ser efectiva, su utilidad puede verse comprometida en casos de disponibilidad limitada de datos. En tales situaciones, existe la posibilidad de que se pierda información relevante durante el entrenamiento, lo que podría resultar en sesgos significativos en los resultados obtenidos.
No obstante, en escenarios donde la cantidad de datos es suficientemente amplia y la distribución entre los conjuntos es equilibrada, este enfoque se muestra completamente apropiado.
6.8.2 Validación cruzada de \(K\) pliegues
La técnica validación cruzada de \(K\) pliegues se caracteriza por su accesibilidad y su reconocimiento generalizado en el ámbito de la validación cruzada. En comparación con otros métodos de validación cruzada, tiende a proporcionar modelos con un menor sesgo (Zhang (1993)).
Esta técnica asegura que todas las observaciones originales de la serie de datos tengan la oportunidad de formar parte, tanto del conjunto de entrenamiento, como del conjunto de prueba. Es especialmente valiosa en situaciones donde los datos de entrada son limitados.
El proceso comienza al dividir de manera aleatoria la serie de datos en \(K\) pliegues. El parámetro \(K\) determina el número de grupos en los que se dividirá la muestra.
Es fundamental elegir un valor adecuado para \(K\), evitando que sea demasiado bajo o demasiado alto. Usualmente, se selecciona un valor entre \(5\) y \(10\) dependiendo del tamaño de la serie de datos. Por ejemplo, si \(K=10\), la serie de datos se divide en \(10\) partes iguales.
Un valor de \(K\) más alto reduce el sesgo del modelo, pero una varianza excesiva puede conducir al sobreajuste. Un valor más bajo equivale prácticamente al enfoque de división de datos en entrenamiento y prueba.
